(本小题满分13分)
已知两个向量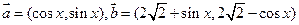 ,f(x)=
,f(x)= 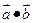 ,
,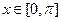
(1)求f(x)的值域;(2)若 ,求
,求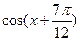 的值
的值
(本小题满分12分)在△ABC中,a, b, c分别为内角A, B, C的对边,且 ,
,
(Ⅰ)求A的大小;
(Ⅱ)求 的最大值.
的最大值.
(本小题12分)设函数 ,其中
,其中 。
。
(1)当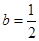 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;
(2)当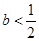 时,求函数
时,求函数 的极值点;
的极值点;
(3)证明:对任意的正整数 ,不等式
,不等式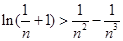 都成立.
都成立.
(本小题12分)在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4.设圆C的半径为1,
圆心在l上.
(1)若圆心C也在直线y=x-1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
(本小题12分)数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, .
.
(1)证明: 是等比数列,并求数列
是等比数列,并求数列 的通项公式
的通项公式 ;
;
(2)设 ,求证:
,求证:
(本小题12分)如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
(1)求证:AC⊥平面BDE;
(2)求二面角FBED的余弦值.