(本小题12分)在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4.设圆C的半径为1,
圆心在l上.
(1)若圆心C也在直线y=x-1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
(1)证明:当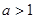 时,不等式
时,不等式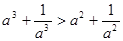 成立;
成立;
(2)要使上述不等式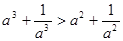 成立,能否将条件“
成立,能否将条件“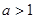 ”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由;
”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由;
(3)请你根据(1)、(2)的证明,试写出一个类似的更为一般的结论,且给予证明.
安排5个大学生到 三所学校支教,设每个大学生去任何一所学校是等可能的.
三所学校支教,设每个大学生去任何一所学校是等可能的.
(1)求5个大学生中恰有2个人去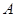 校支教的概率;
校支教的概率;
(2)设有大学生去支教的学校的个数为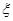 ,求
,求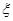 的分布列.
的分布列.
数列 中,
中,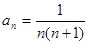 ,前
,前 项的和记为
项的和记为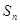 .
.
(1)求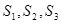 的值,并猜想
的值,并猜想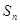 的表达式;
的表达式;
(2)请用数学归纳法证明你的猜想.
三个元件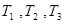 正常工作的概率分别为
正常工作的概率分别为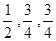 ,将它们中某两个元件并联后再和第三个元件串联接入电路.
,将它们中某两个元件并联后再和第三个元件串联接入电路.
(1)在如图的一段电路中,电路不发生故障的概率是多少?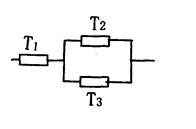
(2)三个元件按要求连成怎样的一段电路时,才能使电路中不发生故障的概率最大?请画出此时的电路图并说明理由.
在二项式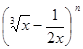 的展开式中,恰好第五项的二项式系数最大.
的展开式中,恰好第五项的二项式系数最大.
(1)求展开式中各项的系数和;
(2)求展开式中的有理项.