如图,在边长为12的正方形A1 AA′A1′中,点B、C在线段AA′上,且AB = 3,BC = 4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P;作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q;将该正方形沿BB1、CC1折叠,使得A′A1′ 与AA1重合,构成如图所示的三棱柱ABC—A1B1C1,在三棱柱ABC—A1B1C1中, (Ⅰ)求证:AB⊥平面BCC1B1; (Ⅱ)求面PQA与面ABC所成的锐二面角的大小.(Ⅲ)求面APQ将三棱柱ABC—A1B1C1分成上、下两部分几何体的体积之比.

 |
|||
 |
|||
已知复数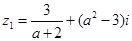 ,
, (
(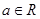 ,
, 是虚数单位).
是虚数单位).
(1)若复数 在复平面上对应点落在第一象限,求实数
在复平面上对应点落在第一象限,求实数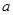 的取值范围;
的取值范围;
(2)若虚数 是实系数一元二次方程
是实系数一元二次方程 的根,求实数
的根,求实数 值.
值.
⑴用综合法证明: ;
;
⑵用反证法证明:若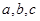 均为实数,且
均为实数,且 ,
, ,
,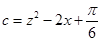 ,求证
,求证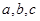 中至少有一个大于0.
中至少有一个大于0.
已知函数f(x)=x2+ax+b,g(x)=ex(cx+d).若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(1)求a,b,c,d的值;
(2)若x≥-2时,f(x)≤kg(x),求k的取值范围.
在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos 2A-3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5 ,b=5,求sin Bsin C的值.
,b=5,求sin Bsin C的值.
已知向量a=(cos 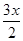 ,sin
,sin 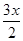 ),b=(-sin
),b=(-sin 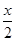 ,-cos
,-cos 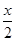 ),其中x∈[
),其中x∈[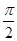 ,π].
,π].
(1)若|a+b|= ,求x的值;
,求x的值;
(2)函数f(x)=a·b+|a+b|2,若c>f(x)恒成立,求实数c的取值范围.