已知点P(x1,y1),Q(x2,y2)是函数f(x)=sin(ωx+Φ)(ω>0,0<Φ< )图象上的任意两点,若|y1-y2|=2时,|x1-x2|的最小值为
)图象上的任意两点,若|y1-y2|=2时,|x1-x2|的最小值为 ,且函数f(x)的图象经过点(0,2),在△ABC中,角A,B,C的对边分别为a,b,c,且2sinAsinC+cos2B=1.
,且函数f(x)的图象经过点(0,2),在△ABC中,角A,B,C的对边分别为a,b,c,且2sinAsinC+cos2B=1.
(1)求函数f(x)的解析式;
(2)求g(B)= f(B)+f(B+
f(B)+f(B+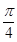 )的取值范围.
)的取值范围.
设函数f(x)=lg( (a>1>b>0),当a,b满足什么关系时,f(x)在(1,+∞)上恒取正值?
(a>1>b>0),当a,b满足什么关系时,f(x)在(1,+∞)上恒取正值?
已知函数f(x)="lg(a" x +ax+1)。(1)若f(x)的定义域R,求实数a的取值范围;(2)若f(x)的值域为R,求实数a的取值范围。
+ax+1)。(1)若f(x)的定义域R,求实数a的取值范围;(2)若f(x)的值域为R,求实数a的取值范围。
已知y= log 的定义域为R,则实数m的取值范围是
的定义域为R,则实数m的取值范围是
| A.m=0, | B.m>-1, | C.-1<m<3, | D.m<-1或m>3。 |
B(文)设 是定义在
是定义在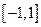 上的偶函数,当
上的偶函数,当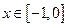 时,
时,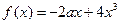 222233.
222233.
(1)若 在
在 上为增函数,求
上为增函数,求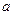 的取值范围;
的取值范围;
(2)是否存在正整数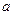 ,使
,使 的图象的最高点落在直线
的图象的最高点落在直线 上?若存在,求出
上?若存在,求出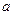 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分12分)A(理)已知函数 ,其中
,其中 .
.
(1)若存在 ,使得
,使得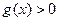 成立,求实数
成立,求实数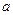 的取值范围;
的取值范围;
(2)求函数 的值域.
的值域.