将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中,将3次遇到黑色障碍物,最后落入
袋或
袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是.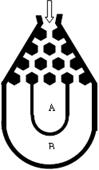
（Ⅰ）求小球落入袋中的概率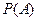
;
（Ⅱ）在容器入口处依次放入4个小球,记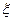
为落入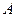袋中小球的个数,试求
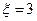的概率和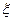的数学期望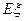
.
已知抛物线
，直线
，
是抛物线的焦点。
（1）在抛物线上求一点
，使点到直线
的距离最小；
(2)如图，过点作直线交抛物线于A、B两点.
①若直线AB的倾斜角为
，求弦AB的长度；
②若直线AO、BO分别交直线于
两点,求
的最小值.
已知函数
,曲线
在点
处切线方程为
.
(1)求
的值；
(2)讨论
的单调性,并求的极小值。
某工厂有一批货物由海上从甲地运往乙地，已知轮船的最大航行速度为60海里/小时，甲地至乙地之间的海上航行距离为600海里，每小时的运输成本由燃料费和其他费用组成，轮船每小时的燃料费与轮船速度的平方成正比，比例系数为0.5，其余费用为每小时1250元。
(1)把全程运输成本
（元）表示为速度
（海里/小时）的函数；
(2)为使全程运输成本最小，轮船应以多大速度行驶？
已知
函数
在
上是单调递减函数,
方程
无实根，若“
或
”为真，“且”为假，求
的取值范围。
已知函数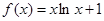
（1）求函数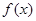
在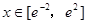
上的最大值与最小值；
（2）若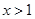
时，函数
的图像恒在直线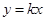
上方，求实数
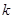的取值范围；
（3）证明：当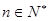
时，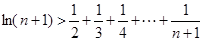
．