已知A.B是椭圆 上两点,O是坐标原点,定点
上两点,O是坐标原点,定点 ,向量
,向量 .
. 在向量
在向量 方向上的投影分别是m.n ,且
方向上的投影分别是m.n ,且 7mn ,动点P满足
7mn ,动点P满足
(Ⅰ)求点P的轨迹C的方程;
(Ⅱ)设过点E的直线l与C交于两个不同的点M.N,求 的取值范围。
的取值范围。
已知函数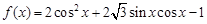
(Ⅰ)求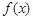 的最小正周期;
的最小正周期;
(Ⅱ)在△ABC中,角A,B,C所对的边分别是 ,
, ,
,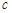 ,若
,若 且
且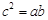 ,
,
试判断△ABC的形状.
某工厂有A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天8h计算,若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排利润最大?
已知函数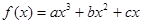 在点
在点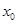 处取得极小值-4,使其导数
处取得极小值-4,使其导数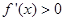 的
的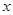 的取值范围为
的取值范围为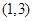 ,求:
,求:
(1)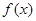 的解析式;
的解析式;
(2) ,求
,求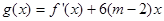 的最大值;
的最大值;
已知:A、B、C是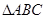 的内角,
的内角,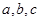 分别是其对边长,向量
分别是其对边长,向量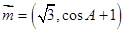 ,
,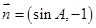 ,
,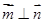 .
.
(Ⅰ)求角A的大小;
(Ⅱ)若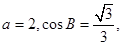 求
求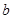 的长.
的长.
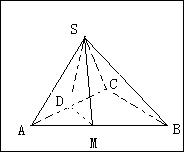
如图平面SAC⊥平面ACB,ΔSAC是边长为4的等边三角形,ΔACB为直角三角形,∠ACB=90°,BC=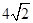 ,求二面角S-AB-C的余弦值。
,求二面角S-AB-C的余弦值。