如图,在正四棱台内,以小底为底面。大底面中心为顶点作一内接棱锥. 已知棱台小底面边长为b,大底面边长为a,并且棱台的侧面积与内接棱锥的侧面面积相等,求这个棱锥的高,并指出有解的条件.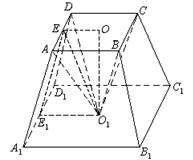
(本小题满分14分)如图,△ABC为一个等腰三角形形状的空地,腰CA的长为3(百米),底AB的长为4(百米).现决定在该空地内筑一条笔直的小路EF(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为S1和S2.
(1) 若小路一端E为AC的中点,求此时小路的长度;
(2) 求 的最小值.
的最小值.
(本小题满分14分)如图,已知四面体ABCD的四个面均为锐角三角形,E、F、G、H分别为边AB、BC、CD、DA上的点,BD∥平面EFGH,且EH=FG.
(1) 求证:HG∥平面ABC;
(2) 请在面ABD内过点E作一条线段垂直于AC,并给出证明.
(本小题满分14分)在△ABC中,角A、B、C的对边分别为a、b、c.
(1) 若sin =2cos A,求A的值;
=2cos A,求A的值;
(2) 若cosA=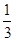 ,b=3c,求sinC的值.
,b=3c,求sinC的值.
(本小题满分10分)选修4-5:不等式选讲。设函数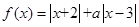
(Ⅰ)当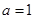 时,求函数
时,求函数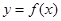 的最小值,并指出取得最小值时
的最小值,并指出取得最小值时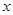 的值;
的值;
(Ⅱ)若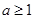 ,讨论关于
,讨论关于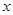 的方程
的方程 =
= 的解的个数.
的解的个数.
(本小题满分10分)选修4-4:坐标系与参数方程
已知极坐标系的极点在直角坐标系的原点处,极轴与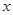 轴的正半轴重合,曲线C1
轴的正半轴重合,曲线C1 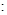
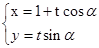 (t为参数),曲线
(t为参数),曲线 .
.
(Ⅰ)写出C1与C2的普通方程;
(Ⅱ)过坐标原点O做C1的垂线,垂足为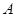 ,P为OA中点,当
,P为OA中点,当 变化时,求P点的轨迹的参数方程,并指出它是什么曲线.
变化时,求P点的轨迹的参数方程,并指出它是什么曲线.