平面直角坐标系有点
(1)求向量 的夹角
的夹角 的余弦用x表示的函数
的余弦用x表示的函数 ;
;
(2)求 的最值、
的最值、
(本小题满分14分)
已知数列 中,
中,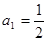 ,
,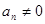 ,
, 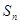 为该数列的前
为该数列的前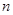 项和,且
项和,且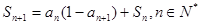 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若不等式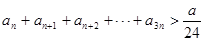 对一切正整数
对一切正整数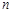 都成立,求正整数
都成立,求正整数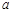 的最大值,并证明结论.
的最大值,并证明结论.
(本小题共14分)如图,四棱锥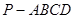 中,底面
中,底面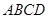 为平行四边形,
为平行四边形,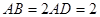 ,
,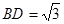 ,
, ⊥底面
⊥底面 .
.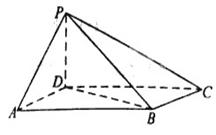
(1)证明:平面 平面
平面 ;
;
(2)若二面角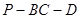 为
为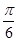 ,求
,求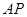 与平面
与平面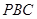 所成角的正弦值。
所成角的正弦值。
(本小题满分12分)
一个口袋内有 (
( )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和 个白球.已知从口袋中随机取出一个球是红球的概率是
个白球.已知从口袋中随机取出一个球是红球的概率是 .
.
(1)当 时,不放回地从口袋中随机取出3个球,求取到白球的个数
时,不放回地从口袋中随机取出3个球,求取到白球的个数 的期望
的期望 ;
;
(2)若 ,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于
,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于 ,求
,求 和
和 .
.
(本小题满分12分)
在 中,角
中,角 的对边分别为
的对边分别为 ,
, 是该三角形的面积,
是该三角形的面积,
(1)若 ,
, ,
, ,求角
,求角 的度数;
的度数;
(2)若 ,
, ,
, ,求
,求 的值.
的值.
(本小题满分14分)
已知函数
(Ⅰ)当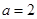 时,解不等式
时,解不等式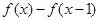 >
>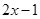 ;
;
(Ⅱ)讨论函数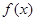 的奇偶性,并说明理由.
的奇偶性,并说明理由.