椭圆G: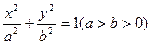 的两个焦点F1(-c,0)、F2(c,0),M是椭圆上的一点,且满足
的两个焦点F1(-c,0)、F2(c,0),M是椭圆上的一点,且满足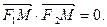
(Ⅰ)求离心率e的取值范围;
(Ⅱ)当离心率e取得最小值时,点N(0,3)到椭圆上的点的最远距离为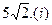 求此时椭圆G的方程;(ⅱ)设斜率为k(k≠0)的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,问A、B两点能否关于过点
求此时椭圆G的方程;(ⅱ)设斜率为k(k≠0)的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,问A、B两点能否关于过点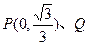 的直线对称?若能,求出k的取值范围;若不能,请说明理由
的直线对称?若能,求出k的取值范围;若不能,请说明理由
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC= ,AD=1.
,AD=1.
(I)求证:CD⊥平面PAC;
(II)求二面角A-PD-C的余弦值.
已知角A,B,C是△ABC三边a,b,c所对的角, ,
, ,
, ,且
,且 .
.
(I)若△ABC的面积S= ,求b+c的值;
,求b+c的值;
(II)求b+c的取值范围.
已知在等差数列{ }中,
}中, =3,前7项和
=3,前7项和 =28.
=28.
(I)求数列{ }的公差d;
}的公差d;
(II)若数列{ }为等比数列,且
}为等比数列,且 ,
, 求数列
求数列 的前n项和
的前n项和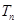
 .
.
设正有理数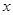 是
是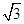 的一个近似值,令
的一个近似值,令 .
.
(Ⅰ)若 ,求证:
,求证: ;
;
(Ⅱ)比较 与
与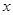 哪一个更接近
哪一个更接近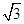 ,请说明理由.
,请说明理由.
在直角坐标系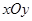 中,已知圆
中,已知圆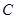 的参数方程
的参数方程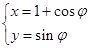 (
(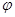 为参数),以
为参数),以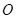 为极点,
为极点,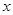 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆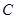 的极坐标方程;
的极坐标方程;
(Ⅱ)直线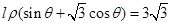 ,射线
,射线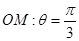 与圆
与圆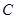 的交点为
的交点为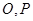 ,与直线
,与直线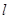 的交点为
的交点为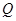 ,求线段
,求线段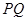 的长.
的长.