在 中,三边
中,三边 、
、 、
、 对角分别为
对角分别为 、
、 、
、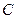 ,且
,且
(1)求角 的余弦值;(2)若
的余弦值;(2)若 ,且
,且 ,求
,求 和
和 的值.
的值.
(本小题满分12分)
设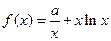 ,
, .
.
(1)当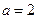 时,求曲线
时,求曲线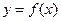 在
在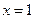 处的切线方程;
处的切线方程;
(2)如果存在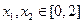 ,使得
,使得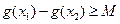 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数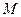 ;
;
(3)如果对任意的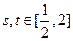 ,都有
,都有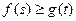 成立,求实数
成立,求实数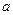 的取值范围.
的取值范围.
(本小题满分12分)
已知椭圆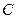 的中心在原点,焦点在
的中心在原点,焦点在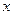 轴上,点
轴上,点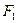 、
、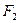 分别是椭圆的左、右焦点,在椭圆
分别是椭圆的左、右焦点,在椭圆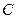 的右准线上的点
的右准线上的点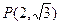 ,满足线段
,满足线段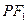 的中垂线过点
的中垂线过点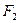 .直线
.直线 :
: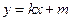 为动直线,且直线
为动直线,且直线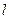 与椭圆
与椭圆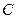 交于不同的两点
交于不同的两点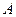 、
、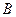 .
.
(1)求椭圆C的方程;
(2)若在椭圆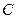 上存在点
上存在点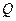 ,满足
,满足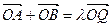 (
(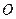 为坐标原点),求实数
为坐标原点),求实数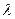 的取值范围;
的取值范围;
(3)在(Ⅱ)的条件下,当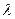 取何值时,
取何值时, 的面积最大,并求出这个最大值.
的面积最大,并求出这个最大值.
已知数列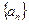 中,
中, ,且当
,且当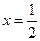 时,函数
时,函数 取得极值。
取得极值。
(1)若 ,求数列
,求数列 的通项公式;
的通项公式;
(2)设数列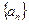 的前
的前 项和为
项和为 ,试证明:
,试证明: 时,
时, .
.
在高中“自选模块”考试中,某考场的每位同学都选了一道数学题,第一小组选《数学史与不等式选讲》的有1人,选《矩阵变换和坐标系与参数方程》的有5人,第二小组选《数学史与不等式选讲》的有2人,选《矩阵变换和坐标系与参数方程》的有4人,现从第一、第二两小组各任选2人分析得分情况
(1)求选出的4 人均为选《矩阵变换和坐标系与参数方程》的概率;
(2)设 为选出的4个人中选《数学史与不等式选讲》的人数,求
为选出的4个人中选《数学史与不等式选讲》的人数,求 的分布列和数学期望
的分布列和数学期望
如图,侧棱垂直底面的三棱柱 的底面
的底面 位于平行四边形
位于平行四边形 中,
中,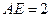 ,
, ,
, ,点
,点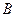 为
为 中点.
中点.
(1)求证:平面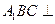 平面
平面 .
.
(2)设二面角 的大小为
的大小为 ,直线
,直线 与平面
与平面 所
所
成的角为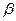 ,求
,求 的值.
的值.