已知数列 满足:
满足: ,且
,且
 (
( ).
). 
(Ⅰ)求证:数列 为等差数列;
为等差数列;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)求下表中前 行所有数的和
行所有数的和 .
.
设A(x1,y1)、B(x2,y2)两点在抛物线y=2x2上,l是AB的垂直平分线.
(1)当且仅当x1+x2取何值时,直线l经过抛物线的焦点F?证明你的结论.
(2)当直线l的斜率为2时,求l在y轴上的截距的取值范围.
过抛物线y2=2px(p>0)上一定点P(x0,y0)(y0>0)作两条直线分别交抛物线于A(x1,y1)、B(x2,y2).
(1)求该抛物线上纵坐标为 的点到其焦点F的距离;
的点到其焦点F的距离;
(2)当PA与PB的斜率存在且倾斜角互补时,求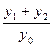 的值,并证明直线AB的斜率是非零常数.
的值,并证明直线AB的斜率是非零常数.
已知抛物线y2=2px(p>0)过动点M(a,0)且斜率为1的直线l与该抛物线交于不同的两点A、B,|AB|≤2p.
(1)求实数a的取值范围;
(2)若线段AB的垂直平分线交x轴于点N,求△NAB面积的最大值.
过抛物线y2=4x的准线与对称轴的交点作直线,交抛物线于M、N两点,问直线的倾斜角多大时,以线段MN为直径的圆经过抛物线的焦点?
某电厂冷却塔外形是如图1-7-8所示的双曲线的一部分绕其中轴(双曲线的虚轴)旋转所成的曲面,其中A,A′是双曲线的顶点,C,C′是冷却塔上口直径的两个端点,B,B′是冷却塔下底直径的两个端点,已知AA′="14" m,CC′="18" m,BB′="22" m,塔高20 m.
图1-7-8
(1)建立坐标系并写出该曲线的方程;
(2)求冷却塔的容积(精确到10 m3,塔壁厚度不计,π取3.14).