如图,在 四棱锥P-ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=AD.
四棱锥P-ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=AD.
(1)求证:EF∥平面PAD;
(2)求证:直线CD⊥平面PAD
(3)求证:面PAD⊥平面PCD.
若函数 =
=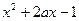 的图象过点
的图象过点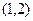
(1)求函数 的解析式;
的解析式;
(2)求函数 在区间
在区间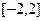 上的最小值和最大值.
上的最小值和最大值.
已知复数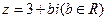 ,且
,且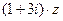 为纯虚数.
为纯虚数.
(1)求复数 ;
;
(2)若 ,求复数
,求复数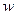 的模
的模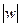 .
.
设全集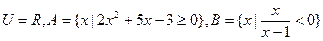
求(1) (2)CU(
(2)CU(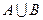 )
)
已知在棱长为 的正方体
的正方体 中,
中, 为棱
为棱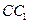 的中点,
的中点, 为正方形
为正方形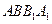 的中心,点
的中心,点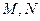 分别在直线
分别在直线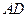 和
和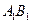 上.
上.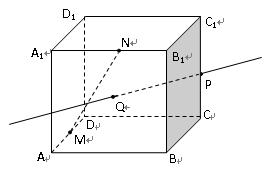
(1)若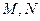 分别为棱
分别为棱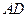 ,
,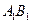 的中点,求直线
的中点,求直线 与
与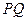 所成角的余弦值;
所成角的余弦值;
(2)若直线 与直线
与直线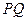 垂直相交,求此时线段
垂直相交,求此时线段 的长;
的长;
(3)在(2)的条件下,求直线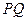 与
与 所确定的平面与平面
所确定的平面与平面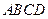 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为 ,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用
,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用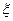 表示取球终止所需要的取球次数.
表示取球终止所需要的取球次数.
(1)求袋中原有白球的个数;
(2)求随机变量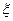 的概率分布;
的概率分布;
(3)求甲取到白球的概率.