设函数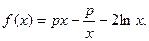
(Ⅰ)若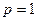 ,函数
,函数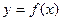 是否有极值,若有则求出极值,若没有,请说明理由.
是否有极值,若有则求出极值,若没有,请说明理由.
(Ⅱ)若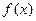 在其定义域内为单调函数,求实数p的取值范围.
在其定义域内为单调函数,求实数p的取值范围.
已知不等式 的解集为
的解集为 ,求不等式
,求不等式 的解集.
的解集.
已知函数f(x)=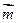 ·
·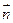 ,其中
,其中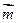 =(sinωx+cosωx,
=(sinωx+cosωx,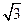 cosωx),
cosωx),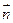 =cosωx-sinωx,2sinωx)(ω>0),若f(x)相邻的对称轴之间的距离不小于
=cosωx-sinωx,2sinωx)(ω>0),若f(x)相邻的对称轴之间的距离不小于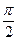 .
.
(1)求ω的取值范围;
(2)在△ABC中,a,b,c分别为A,B,C的对边,a=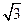 ,b+c=3,当ω最大时,f(A)=1,求△ABC的面积.
,b+c=3,当ω最大时,f(A)=1,求△ABC的面积.
在△ABC中,角A、B、C所对边分别为a,b,c,已知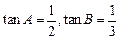 ,且最长边的边长为l.求:
,且最长边的边长为l.求:
(I)角C的大小;
(II)△ABC最短边的长.
解关于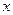 的不等式:
的不等式: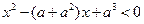
(本小题12分)
如图,曲线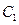 是以原点
是以原点 为中心,以
为中心,以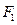 、
、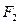 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线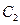 是以
是以 为顶点,以
为顶点,以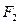 为焦点的抛物线的一部分,
为焦点的抛物线的一部分, 是曲线
是曲线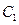 和
和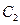 的交点,且
的交点,且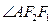 为钝角,若
为钝角,若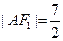 ,
,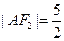 .
.
(I)求曲线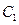 和
和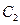 所在的椭圆和抛物线的方程;
所在的椭圆和抛物线的方程;
(II)过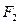 作一条与轴不垂直的直线,分别与曲线
作一条与轴不垂直的直线,分别与曲线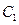 、
、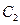 依次交于
依次交于 、
、 、
、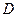 、
、 四点(如图),若
四点(如图),若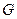 为
为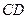 的中点,
的中点,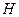 为
为 的中点,问
的中点,问 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由.