(本题满分13分)在一个盒子中,放有标号分别为 ,
,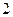 ,
,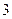 的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为
的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为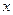 、
、 ,记
,记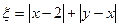 .(1)求随机变量
.(1)求随机变量 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率;(2)求随机变量
取得最大值”的概率;(2)求随机变量 的分布列和数学期望.
的分布列和数学期望.
已知 N*)展开式中第五项的系数与第三项的系数之比为
N*)展开式中第五项的系数与第三项的系数之比为 .
.
(1)求 n的值;
(2)求展开式中含 的项.
的项.
为了调查胃病是否与生活规律有关,调查某地540名40岁以上的人得结果如下:
根据以上数据回答40岁以上的人患胃病与生活规律有关吗?
已知 (m
(m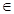 R)
R)
(1)若函数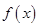 在
在 上单调递增,求实数
上单调递增,求实数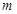 的取值范围;
的取值范围;
(2)当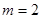 时,求函数
时,求函数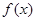 在
在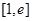 上的最大,最小值;
上的最大,最小值;
(3)求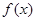 的单调区间.
的单调区间.
一台机器可以按各种不同的速度运转,其生产的物件有一些会有问题,每小时生产有问题物件的多寡,随机器运转的速度而变化,下面表格中的数据是几次试验的结果.
| 速度(转/秒) |
每小时生产有问题物件数 |
| 8 |
5 |
| 12 |
8 |
| 14 |
9 |
| 16 |
11 |
(1)求出机器速度影响每小时生产有问题物件数的回归直线方程;
(2)若实际生产中所允许的每小时最大问题物件数为10,那么机器的速度不得超过多少转/秒?
某项选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考试,否则即被淘汰,已知某选手能正确回答第一、二、三轮的问题的概率分别为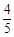 、
、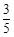 、
、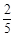 ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手被淘汰的概率;
(Ⅱ)该选手在选拔中回答问题的个数记为ξ,求随机变量ξ的分布列与数学期望.(注:本小题结果可用分数表示)