(本题满分16分,第(1)小题6分,第(2)小题10分)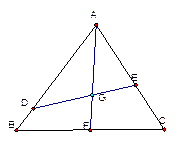
如图,已知点 是边长为
是边长为 的正三角形
的正三角形 的中心,线段
的中心,线段 经过点
经过点 ,并绕点
,并绕点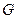 转动,分别交边
转动,分别交边 、
、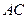 于点
于点 、
、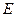 ;设
;设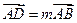 ,
,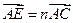 ,其中
,其中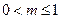 ,
,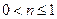 .
.
(1)求表达式 的值,并说明理由;
的值,并说明理由;
(2)求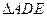 面积的最大和最小值,并指出相应的
面积的最大和最小值,并指出相应的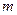 、
、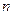 的值.
的值.
已知B(-6,0),C(6,0)是三角形ABC的两个顶点,内角A、B、C满足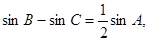 ,求顶点A运动的轨迹方程.
,求顶点A运动的轨迹方程.
(1)若抛物线过直线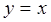 与圆
与圆 的交点, 且顶点在原点,坐标轴为对称轴,求抛物线的方程.
的交点, 且顶点在原点,坐标轴为对称轴,求抛物线的方程.
(2)已知双曲线与椭圆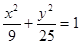 共焦点,它们的离心率之和为
共焦点,它们的离心率之和为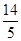 ,求双曲线方程.
,求双曲线方程.
已知p:方程x2+mx+1=0有两个不等的负根;q:方程4x2+4(m-2)x+1=0无实根.若“p或q”为真,“p且q”为假,求m的取值范围.
已知命题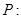 “若
“若 则二次方程
则二次方程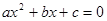 没有实根”.
没有实根”.
(1)写出命题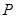 的否命题; (2)判断命题
的否命题; (2)判断命题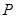 的否命题的真假, 并证明你的结论
的否命题的真假, 并证明你的结论
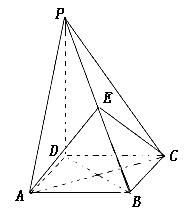
如图,四棱锥 的底面是正方形,
的底面是正方形,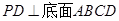 ,点E在棱PB上.
,点E在棱PB上.
(1)求证:平面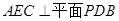 ;
;
(2)当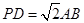 且E为PB的中点时,求AE与平面PDB所成的角的大小.
且E为PB的中点时,求AE与平面PDB所成的角的大小.