(本题满分10分)已知函数f(x)=3x,且 (18)=a+2,g(x)=
(18)=a+2,g(x)=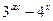
⑴ 求a的值;
⑵ 求g(x)的表达式;
⑶ 当x∈[-1,1]时,g(x)的值域并判断g(x)的单调性.
已知数列{an}是公比为q的等比数列,Sn是其前n项和,且S3,S9,S6成等差数列
(1)求证:a2 , a8, a5也成等差数列
(2)判断以a2, a8, a5为前三项的等差数列的第四项是否也是数列{an}中的一项,若是求出这一项,若不是请说明理由
若数列 前n项和可表示为
前n项和可表示为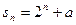 ,则
,则 是否可能成为等比数列?若可能,求出a值;若不可能,说明理由
是否可能成为等比数列?若可能,求出a值;若不可能,说明理由
已知二次函数f(x)=ax2+bx,且f(x+1)为偶函数,定义:满足f(x)=x的实数x称为函数f(x)的不动点,若函数f(x)有且仅有一个不动点,
(1)求f(x)的解析式;
(2)若函数g(x)= f(x)+ +
+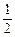 x2在 (0,
x2在 (0, ]上是单调减函数,求实数k的取值范围;
]上是单调减函数,求实数k的取值范围;
(3)在(2)的条件下,是否存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由。
已知集合P=[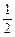 ,2],函数y= log2(ax2-2x+2)的定义域为Q。
,2],函数y= log2(ax2-2x+2)的定义域为Q。
(1)若P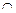 Q
Q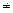
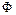 ,求实数a的取值范围;
,求实数a的取值范围;
(2)若方程log2(ax2-2x+2)=2在[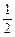 ,2]内有解,求实数a的取值范围。
,2]内有解,求实数a的取值范围。
某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图1所示的一条折线表示:西红柿的种植成本与上市时间的关系用图2所示的抛物线表示。(注:市场售价和种植成本的单位:元/102kg,时间单位:天)
(1)写出图1表示的市场售价与时间的函数关系式P=f(t);写出图2表示的种植成本与时间的函数关系式Q=g(t);
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?为多少?
图1图2