已知数列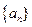 满足,
满足,  .
. 令
令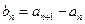 ,证明:
,证明: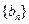 是等比数列; (Ⅱ)求
是等比数列; (Ⅱ)求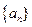 的通项公式。
的通项公式。
设数列 满足a1=0且
满足a1=0且 -
-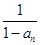 = 1.
= 1.
(1) 求 的通项公式;
的通项公式;
(2) 设bn= ,记Sn=
,记Sn= ,证明:Sn<1.
,证明:Sn<1.
设同时满足条件:① ≤bn+1(n∈N*);②bn≤M(n∈N*,M是与n无关的常数)的无穷数列{bn}叫“特界” 数列.
≤bn+1(n∈N*);②bn≤M(n∈N*,M是与n无关的常数)的无穷数列{bn}叫“特界” 数列.
(1) 若数列{an}为等差数列,Sn是其前n项和,a3=4,S3=18,求Sn;
(2) 判断(1)中的数列{Sn}是否为“特界” 数列,并说明理由.
已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P为椭圆上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN,那么kPM与kPN之积是与点P位置无关的定值.试对双曲线 =1写出具有类似特性的性质,并加以证明.
=1写出具有类似特性的性质,并加以证明.
在各项为正的数列{an}中,数列的前n项和Sn满足Sn= .
.
(1) 求a1,a2,a3;
(2) 由(1)猜想数列{an}的通项公式;
(3) 求Sn.
如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用S平方米塑料片制成圆柱的侧面和下底面(不安装上底面).当圆柱底面半径r取何值时,S取得最大值?并求出该最大值(结果精确到0.01平方米).