设同时满足条件：①
≤bn＋1(n∈N*)；②bn≤M(n∈N*，M是与n无关的常数)的无穷数列{bn}叫“特界” 数列．
(1) 若数列{an}为等差数列，Sn是其前n项和，a3＝4，S3＝18，求Sn；
(2) 判断(1)中的数列{Sn}是否为“特界” 数列，并说明理由．
袋中有8个大小相同的小球，其中1个黑球，3个白球，4个红球.
（I）若从袋中一次摸出2个小球，求恰为异色球的概率；
（II）若从袋中一次摸出3个小球，且3个球中，黑球与白球的个数都没有超过红球的个数，记此时红球的个数为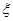
，求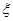的分布列及数学期望E.
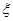已知向量
，
，设函数
，
.
（Ⅰ）求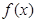
的最小正周期与最大值；
（Ⅱ）在
中，
分别是角
的对边，若
的面积为
，求
的值.
设函数
.（Ⅰ）当
时，解不等式
；
（Ⅱ）当
时，不等式
的解集为
，求实数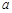
的取值范围.
直角坐标系
中，曲线
的参数方程为
（
为参数），直线
的参数方程为
（
为参数），
为直线与曲线的公共点. 以原点
为极点，
轴的正半轴为极轴建立极坐标系.
（Ⅰ）求点的极坐标；
（Ⅱ）将曲线上所有点的纵坐标伸长为原来的
倍（横坐标不变）后得到曲线
，过点作直线
，若直线被曲线截得的线段长为
，求直线的极坐标方程.
已知函数
在
处取得极值．
（Ⅰ）求
的值；
（Ⅱ）证明：当
时，
.