在复数范围内解方程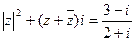 (i为虚数单位).
(i为虚数单位).
设函数 的定义域为A,函数
的定义域为A,函数 的定义域为B.
的定义域为B.
(1)若 ,求实数a的取值范围;
,求实数a的取值范围;
(2)设全集为R,若非空集合 的元素中有且只有一个是整数,求实数a的取值范围.
的元素中有且只有一个是整数,求实数a的取值范围.
已知函数 ,当
,当 时,恒有
时,恒有 .
.
(1)求 的表达式及定义域;
的表达式及定义域;
(2)若方程 有解,求实数
有解,求实数 的取值范围;
的取值范围;
(3)若方程 的解集为
的解集为 ,求实数
,求实数 的取值范围.
的取值范围.
已知 ,m是是实常数.
,m是是实常数.
(1)当m=1时,写出函数 的值域;
的值域;
(2)当m=0时,判断函数 的奇偶性,并给出证明;
的奇偶性,并给出证明;
(3)若 是奇函数,不等式
是奇函数,不等式 对
对 恒成立,求a的取值范围.
恒成立,求a的取值范围.
若二次函数f(x)=ax2+bx+c (a≠0)满足f(x+1)-f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)若在区间[-1,1]上,不等式f(x)>2x+m恒成立,求实数m的取值范围.
已知sin -2cos
-2cos =0.
=0.
(1)求tanx的值;
(2)求 的值.
的值.