(本小题满分12分)
某商店经销一种奥运纪念品,每件产品成本为30元,且每卖出一件产品,需向税务部门上交 元(
元( 为常数,
为常数,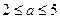 )的税收,设每件产品的日售价为
)的税收,设每件产品的日售价为 元(
元( ),根据市场调查,日销售量与
),根据市场调查,日销售量与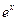 (
( 为自然对数的底数)成反比,已知每件产品的日售价为40元,日销售量为10件。w.w.w求商店的日利润
为自然对数的底数)成反比,已知每件产品的日售价为40元,日销售量为10件。w.w.w求商店的日利润 元与每件产品的日售价
元与每件产品的日售价 元的函数关系式;当每件产品的日售价为多少元时该商店的日利润
元的函数关系式;当每件产品的日售价为多少元时该商店的日利润 最大,说明理由。
最大,说明理由。
(本小题满分15分)
设函数 与
与 的图像分别交直线
的图像分别交直线 于点
于点 ,且曲线
,且曲线 在点
在点 处的切线与曲线
处的切线与曲线 在点
在点 处的切线平行.
处的切线平行.
(1)求函数 ,
, 的表达式;
的表达式;
(2)设函数 ,求函数
,求函数 的最小值;
的最小值;
(3)若不等式 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
(本小题满分14分)
如图所示,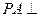 平面
平面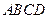 ,底面
,底面 为菱形,
为菱形,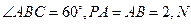 为
为 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证: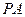 //平面
//平面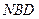 ;
;
(3) 求二面角 的平面角的大小.
的平面角的大小.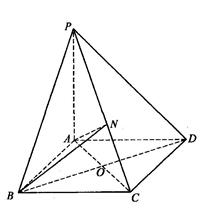
.(本小题满分14分)
已知单调递增的等比数列 满足:
满足: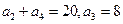 ;
;
(1)求数列 的通项公式;
的通项公式;
(2)若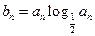 ,数列
,数列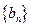 的前n项和为
的前n项和为 ,求
,求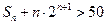 成立的正整数 n的最小值.
成立的正整数 n的最小值.
(本小题满分14分)在△ABC中,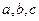 分别为角A、B、C的对边,
分别为角A、B、C的对边, ,
, ="3," △ABC的面积为6.
="3," △ABC的面积为6.
⑴角A的正弦值;⑵求边 b、c.
b、c.
设函数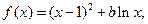 其中
其中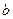 为常数.
为常数.
(Ⅰ)若函数 有极值点,求
有极值点,求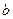 的取值范围及
的取值范围及 的极值点
的极值点 ;
;
(Ⅱ)证明:对任意不小于3的正整数 ,不等式
,不等式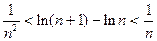 都成立.
都成立.