如图所示,在直角梯形ABCP中,AB=BC=3,AP=7,CD⊥AP,现将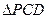 沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。
沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。
(I)求证:PA//平面EFG;
(II)若M为线段CD上的一个动点,问当M在什么位置时,MF与平面EFG所成角最大。
已知直线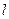 的参数方程为
的参数方程为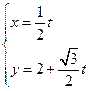 (t为参数),曲线C的极坐标方程是
(t为参数),曲线C的极坐标方程是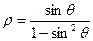 以极点为原点,极轴为x轴正方向建立直角坐标系,点
以极点为原点,极轴为x轴正方向建立直角坐标系,点 ,直线
,直线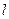 与曲
与曲
线C交于A,B两点.
(1)写出直线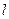 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
(2)线段MA,MB长度分别记|MA|,|MB|,求|MA|·|MB|的值.
某校高三某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
(1)求分数在[50,60)的频率及全班人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
已知函数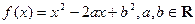 .
.
(1)若从集合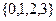 中任取一个元素
中任取一个元素 ,从集合
,从集合 中任取一个元素
中任取一个元素 ,求方程
,求方程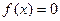 有两个不相等实根的概率;
有两个不相等实根的概率;
(2)若 是从区间
是从区间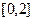 中任取的一个数,
中任取的一个数, 是从区间
是从区间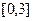 中任取的一个数,求方程
中任取的一个数,求方程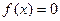 没有实根的概率.
没有实根的概率.
已知函数 ,其中
,其中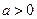 .
.
(1)若 在
在 处取得极值,求
处取得极值,求 的值;
的值;
(2)求 的单调区间;
的单调区间;
(3)若 的最小值为1,求
的最小值为1,求 的取值范围.
的取值范围.
已知 是椭圆
是椭圆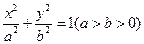 的左、右焦点,过点
的左、右焦点,过点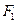 作
作
倾斜角为 的动直线
的动直线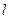 交椭圆于
交椭圆于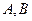 两点.当
两点.当 时,
时, ,且
,且 .
.
(1)求椭圆的离心率及椭圆的标准方程;
(2)求△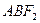 面积的最大值,并求出使面积达到最大值时直线
面积的最大值,并求出使面积达到最大值时直线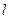 的方程.
的方程.