已知函数 ,其中
,其中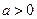 .
.
(1)若 在
在 处取得极值,求
处取得极值,求 的值;
的值;
(2)求 的单调区间;
的单调区间;
(3)若 的最小值为1,求
的最小值为1,求 的取值范围.
的取值范围.
在正三棱柱ABCA1B1C1中,点D是BC的中点,BC=BB1.
(1)若P是CC1上任一点,求证:AP不可能与平面BCC1B1垂直;
(2)试在棱CC1上找一点M,使MB⊥AB1.
在三棱锥SABC中,SA⊥平面ABC,SA=AB=AC=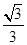 BC,点D是BC边的中点,点E是线段AD上一点,且AE=3DE,点M是线段SD上一点,
BC,点D是BC边的中点,点E是线段AD上一点,且AE=3DE,点M是线段SD上一点,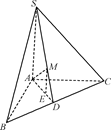
(1)求证:BC⊥AM;
(2)若AM⊥平面SBC,求证:EM∥平面ABS.
已知如图①所示,矩形纸片AA′A1′A1,点B、C、B1、C1分别为AA′、A1A1′的三等分点,将矩形纸片沿BB1、CC1折成如图②形状(正三棱柱),若面对角线AB1⊥BC1,求证:A1C⊥AB1.
(图①)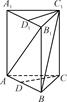
(图②)
如图,在正三棱柱ABCA1B1C1中,A1A=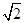 AC,D、E、F分别为线段AC、A1A、C1B的中点.
AC,D、E、F分别为线段AC、A1A、C1B的中点.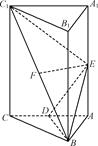
(1)证明:EF∥平面ABC;
(2)证明:C1E⊥平面BDE.
如图,在四棱锥PABCD中,PD⊥底面ABCD,AD⊥AB,CD∥AB,AB=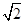 AD=2,CD=3,直线PA与底面ABCD所成角为60°,点M、N分别是PA、PB的中点.求证:
AD=2,CD=3,直线PA与底面ABCD所成角为60°,点M、N分别是PA、PB的中点.求证: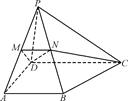
(1)MN∥平面PCD;
(2)四边形MNCD是直角梯形;
(3)DN⊥平面PCB.