在正三棱柱ABCA1B1C1中,点D是BC的中点,BC=BB1.
(1)若P是CC1上任一点,求证:AP不可能与平面BCC1B1垂直;
(2)试在棱CC1上找一点M,使MB⊥AB1.
已知函数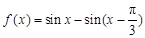 .
.
(1)求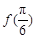 ;
;
(2)求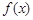 在
在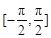 上的取值范围.
上的取值范围.
设不等式组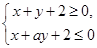 表示的区域为
表示的区域为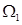 ,不等式
,不等式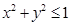 表示的平面区域为
表示的平面区域为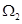 .
.
(1)若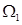 与
与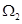 有且只有一个公共点,则
有且只有一个公共点,则 =;
=;
(2)记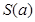 为
为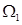 与
与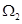 公共部分的面积,则函数
公共部分的面积,则函数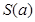 的取值范围是.
的取值范围是.
在平面直角坐标系中,对于任意相邻三点都不共线的有序整点列(整点即横纵坐标都是整数的点) :
: 与
与 :
: ,其中
,其中 ,若同时满足:①两点列的起点和终点分别相同;②线段
,若同时满足:①两点列的起点和终点分别相同;②线段 ,其中
,其中 ,则称
,则称 与
与 互为正交点列.
互为正交点列.
(1)求 :
: 的正交点列
的正交点列 ;
;
(2)判断 :
: 是否存在正交点列
是否存在正交点列 ?并说明理由;
?并说明理由;
(3) N,是否都存在无正交点列的有序整点列
N,是否都存在无正交点列的有序整点列 ?并证明你的结论.
?并证明你的结论.
已知 是椭圆
是椭圆 上两点,点M的坐标为
上两点,点M的坐标为 .
.
(1)当 两点关于
两点关于 轴对称,且
轴对称,且 为等边三角形时,求
为等边三角形时,求 的长;
的长;
(2)当 两点不关于
两点不关于 轴对称时,证明:
轴对称时,证明: 不可能为等边三角形.
不可能为等边三角形.
已知曲线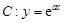 .
.
(1)若曲线C在点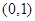 处的切线为
处的切线为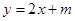 ,求实数
,求实数 和
和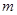 的值;
的值;
(2)对任意实数 ,曲线
,曲线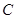 总在直线
总在直线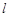 :
: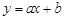 的上方,求实数
的上方,求实数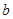 的取值范围.
的取值范围.