已知抛物线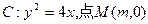 在x轴的正半轴上,过M的直线
在x轴的正半轴上,过M的直线 与C相交于A、B两点,O为坐标原点。
与C相交于A、B两点,O为坐标原点。
(I)若m=1,且直线 的斜率为1,求以AB为直径的圆的方程;
的斜率为1,求以AB为直径的圆的方程;
(II)问是否存在定点M,不论直线 绕点M如何转动,使得
绕点M如何转动,使得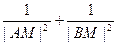 恒为定值。
恒为定值。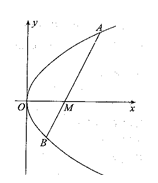
(本小题满分12分)
已知双曲线 的离心率
的离心率 ,其一条准线方程为
,其一条准线方程为 .
.
(Ⅰ)求双曲线 的方程;
的方程;
(Ⅱ)如题20图:设双曲线 的左右焦点分别为
的左右焦点分别为 ,点
,点 为该双曲线右支上一点,直线
为该双曲线右支上一点,直线 与其左支交于点
与其左支交于点 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分12分)
设函数 ,其中
,其中 为常数.
为常数.
(Ⅰ)当 时,判断函数
时,判断函数 的单调性;
的单调性;
(Ⅱ)若函数 在其定义域上既有极大值又有极小值,求
在其定义域上既有极大值又有极小值,求 的取值范围.
的取值范围.
(本小题满分13分)
如题18图,平行六面体 的下底面
的下底面 是边长为
是边长为 的正方形,
的正方形, ,且点
,且点 在下底面
在下底面 上的射影恰为
上的射影恰为
 点.
点.
(Ⅰ)证明: 面
面 ;
;
(Ⅱ)求二面角 的大小.
的大小.
(本小题满分13分)
一个口袋中有大小相同的2个白球和4个黑球,每次从袋中随机地摸出1个球,并换入1只相同大小的黑球,这样继续下去,求:
(Ⅰ)第2次摸出的恰好是白球的概率;
(Ⅱ)摸2次摸出白球的个数 的分布列与数学期望.
的分布列与数学期望.
(本小题满分13分)
已知
 ,若函数
,若函数 的最小正周期为
的最小正周期为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求函数 的单调递增区间.
的单调递增区间.