已知数列{a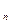 }中,a
}中,a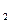 =2,前n项和为S
=2,前n项和为S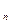 ,且S
,且S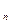 =.
=.
(1)证明数列{an+1-an}是等差数列,并求出数列{an}的通项公式
(2)设bn=,数列{bn}的前n项和为Tn,求使不等式Tn>
对一切n∈N*都成立的最大正整数k的值
已知椭圆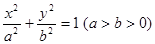 ,点
,点 在椭圆上。
在椭圆上。
(1)求椭圆的离心率;
(2)若椭圆的短半轴长为 ,直线
,直线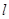 与椭圆交于A、B,且线段AB以M(1,1)为中点,求直线
与椭圆交于A、B,且线段AB以M(1,1)为中点,求直线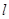 的方程。
的方程。
已知椭圆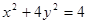 ,直线
,直线 :y=x+m
:y=x+m
(1)若 与椭圆有一个公共点,求
与椭圆有一个公共点,求 的值;
的值;
(2)若 与椭圆相交于P,Q两点,且|PQ|等于椭圆的短轴长,求m的值.
与椭圆相交于P,Q两点,且|PQ|等于椭圆的短轴长,求m的值.
设命题 ;命题
;命题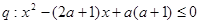 ,若
,若 是
是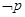 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围。
的取值范围。
若椭圆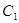 的离心率为
的离心率为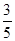 ,焦点在
,焦点在 轴上,且长轴长为10,曲线
轴上,且长轴长为10,曲线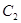 上的点与椭圆
上的点与椭圆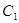 的两个焦点的距离之差的绝对值等于4.
的两个焦点的距离之差的绝对值等于4.
(1)求椭圆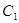 的标准方程;
的标准方程;
(2)求曲线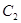 的方程。
的方程。
某商品的市场日需求量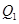 和日产量
和日产量 均为价格
均为价格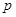 的函数,且
的函数,且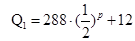
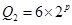 ,日成本C关于日产量
,日成本C关于日产量 的关系为
的关系为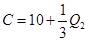
(1)当 时的价格为均衡价格,求均衡价格
时的价格为均衡价格,求均衡价格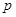 ;
;
(2)当 时日利润
时日利润 最大,求
最大,求