已知函数f(x)=

(1)、求f(2)与f( ),f(3)与f(
),f(3)与f( );
);
(2)、由(1)中求得结果,你能发现f(x) 与f(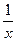 )有什么关系?并证明你的结论;
)有什么关系?并证明你的结论;
(3)、求f(1)+f(2)+f(3)+ 的值.
的值.
求证:经过平面外一点有且只有一个平面和已知平面平行
已知: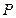
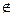 α
α
求证:过点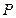 有且只有一个平面β∥α
有且只有一个平面β∥α
已知函数f(x)=logax(a>0,a≠1),如果对于任意x∈[3,+∞)都有|f(x)|≥1成立,
试求a的取值范围.
已知定义在R上的奇函数f(x)有最小正周期2,且当x∈(0,1)时,f(x)=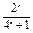 .
.
(1)求f(x)在[-1,1]上的解析式;(2)证明:f(x)在(0,1)上是减函数.
已知函数f(x),当x,y∈R时,恒有f(x+y)=f(x)+f(y).(1)求证:f(x)是奇函数;
(2)如果x∈R+,f(x)<0,并且f(1)=- ,试求f(x)在区间[-2,6]上的最值.
,试求f(x)在区间[-2,6]上的最值.
已知函数f(x)的定义域为R,且满足f(x+2)=-f(x)(1)求证:f(x)是周期函数;(2)若f(x)为奇函数,且当0≤x≤1时,f(x)= x,求使f(x)=-
x,求使f(x)=- 在[0,2 009]上的所有x的个数.
在[0,2 009]上的所有x的个数.