已知函数f(x),当x,y∈R时,恒有f(x+y)=f(x)+f(y).(1)求证:f(x)是奇函数;
(2)如果x∈R+,f(x)<0,并且f(1)=- ,试求f(x)在区间[-2,6]上的最值.
,试求f(x)在区间[-2,6]上的最值.
如图,AB为圆O的直径,点E、F在圆O上,且AB∥EF,矩形ABCD所在的平面与圆O所在的平面互相垂直,已知AB=2,AD=EF=1.
(Ⅰ)设FC的中点为M,求证:OM∥平面DAF;
(Ⅱ)设平面CBF将几何体EF-ABCD分割成的两个锥体的体积分别为VF-ABCD、VF-CBE,求VF-ABCD:VF-CBE的值.
设等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2an+1.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)证明:对一切正整数n,有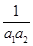 +
+ +…+
+…+ <
< .
.
在△ABC中,角A,B,C的对边分别为a,b,c.已知2cos(B-C)+1=4cosBcosC.
(Ⅰ)求A;
(Ⅱ)若a=2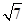 ,△ABC的面积为2
,△ABC的面积为2 ,求b+c.
,求b+c.
已知函数f(x)= +aln(x-1)(a∈R).
+aln(x-1)(a∈R).
(Ⅰ)若f(x)在[2,+∞)上是增函数,求实数a的取值范围;
(Ⅱ)当a=2时,求证:1-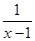 <2ln(x-1)<2x-4(x>2);
<2ln(x-1)<2x-4(x>2);
(Ⅲ)求证: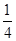 +
+ +…+
+…+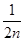 <lnn<1+
<lnn<1+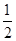 + +
+ +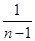 (n∈N*,且n≥2).
(n∈N*,且n≥2).
已知椭圆C: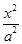 +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1时,坐标原点O到l的距离为
,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1时,坐标原点O到l的距离为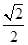 .
.
(Ⅰ)求a,b的值;
(Ⅱ)C上是否存在点P,使得当l绕F转到某一位置时,有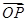 =
= +
+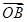 成立?若存在,求出所有的P的坐标与l的方程;若不存在,说明理由.
成立?若存在,求出所有的P的坐标与l的方程;若不存在,说明理由.