(本小题13分)
设等比数列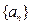 的前项和为
的前项和为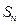 ,首项
,首项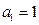 ,公比
,公比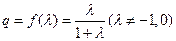 .
.
(I)证明: ;
;
(II)若数列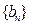 满足
满足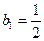 ,
,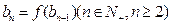 ,求数列
,求数列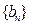 的通项公式;
的通项公式;
(III)记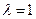 ,
,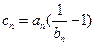 ,数列
,数列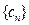 的前项和为
的前项和为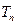 ,求证:当
,求证:当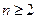 时,
时, .
.
已知函数 .
.
(1)用“五点法”画出函数f(x)在[0, ]上的简图;
]上的简图;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,f(A)=1, ,b+c=3(b>c),求b,c的长.
,b+c=3(b>c),求b,c的长.
已知0<a<1,判断函数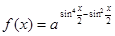 的奇偶性,并求出函数f(x)的周期.
的奇偶性,并求出函数f(x)的周期.
设α∈(0, ),f(x)的定义域为[0,1],f(0)=0,f(1)=1,当x≥y时,有
),f(x)的定义域为[0,1],f(0)=0,f(1)=1,当x≥y时,有 ,求
,求 、
、 .
.
已知函数 .
.
(1)当a=1时,求函数f(x)的单调递增区间;
(2)(ⅰ)当a<0且x∈[0,π]时,函数f(x)的值域是[3,4],求a+b的值;
(ⅱ)当a<0时,函数f(x)的值域是[3,4],求a+b的值.
已知向量a=(cosx,sinx),b=(sin2x,1-cos2x),c=(0,1),x∈(0,π).
(1)向量a、b是否共线?请证明你的结论.
(2)若函数f(x)=|b|-(a+b)·c,求f(x)的最小值,并指出取得最小值时的x值.