在△ABC中,角A、B、C所对边分别为a,b,c,已知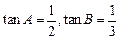 ,且最长边的边长为l.求:
,且最长边的边长为l.求:
(I)角C的大小;
(II)△ABC最短边的长.
如图,在三棱柱 中,侧棱
中,侧棱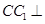 底面
底面 ,
, ,
, ,
, ,
,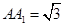 .
.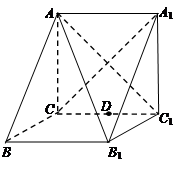
(1)证明: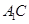
 平面
平面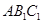 ;
;
(2)若 是棱
是棱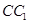 的中点,在棱
的中点,在棱 上是否存在一点
上是否存在一点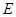 ,使
,使 平面
平面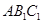 ?证明你的结论.
?证明你的结论.
在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.
(1)求取出的两个球上标号为相邻整数的概率;
(2)求取出的两个球上标号之和能被3整除的概率
已知向量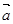 =
=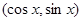 ,
, 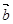 =
=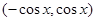 ,
, 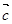 =
=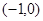
(1)若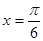 ,求向量
,求向量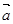 、
、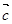 的夹角
的夹角
(2)当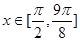 时,求函数
时,求函数 的最大值
的最大值
已知函数 满足
满足 ,
, 且
且 在
在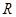 上恒成立.
上恒成立.
(1)求 的值;
的值;
(2)若 ,解不等式
,解不等式 ;
;
(3)是否存在实数 ,使函数
,使函数 在区间
在区间 上有最小值
上有最小值 ?若存在,请求出实数
?若存在,请求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知点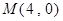 、
、 ,若动点
,若动点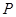 满足
满足 .
.
(1)求动点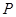 的轨迹曲线
的轨迹曲线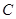 的方程;
的方程;
(2)在曲线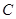 上求一点
上求一点 ,使点
,使点 到直线:
到直线: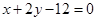 的距离最小.
的距离最小.