已知动点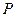 到定点
到定点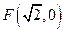 的距离与点
的距离与点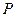 到定直线
到定直线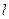 :
: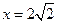 的距离之比为
的距离之比为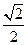 .
.
(1)求动点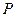 的轨迹
的轨迹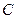 的方程;
的方程;
(2)设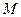 、
、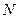 是直线
是直线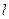 上的两个点,点
上的两个点,点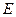 与点
与点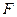 关于原点
关于原点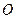 对称,若
对称,若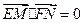 ,求
,求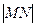 的最小值.
的最小值.
(本小题满分13分)一个袋中有大小相同的标有1,2,3,4,5,6的6个小球,某人做如下游戏,每次从袋中拿一个球(拿后放回),记下标号.若拿出球的标号是3的倍数,则得1分,否则得 分.
分.
(Ⅰ)求拿4次至少得2分的概率;
(Ⅱ)求拿4次所得分数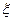 的分布列和数学期望.
的分布列和数学期望.
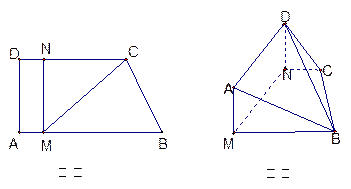
(本小题满分13分)如图甲,直角梯形 中,
中,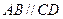 ,
,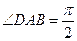 ,点
,点 、
、 分别在
分别在 ,
, 上,且
上,且 ,
,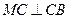 ,
,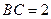 ,
, ,现将梯形
,现将梯形 沿
沿 折起,使平面
折起,使平面 与平面
与平面 垂直(如图乙).
垂直(如图乙).
(Ⅰ)求证: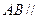 平面
平面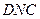 ;
;
(Ⅱ)当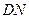 的长为何值时,
的长为何值时,
二面角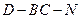 的大小为
的大小为 ?
?
(本小题满分13分)已知
 ,
,
 ,其中
,其中 ,若函数
,若函数
 ,且
,且 的对称中心到
的对称中心到 对称轴的最近距离不小于
对称轴的最近距离不小于
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)在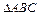 中,
中, 分别是角
分别是角 的对边,且
的对边,且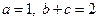 ,当
,当 取最大值时,
取最大值时,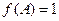 ,求
,求 的面积.
的面积.
(本小题满分14分)
已知函数 有如下性质:如果常数
有如下性质:如果常数 ,那么该函数在
,那么该函数在 上是减函数,
上是减函数,
在 上是增函数,
上是增函数,

(Ⅰ)如果函数 的值域是
的值域是 ,求实数
,求实数 的值;
的值;
(Ⅱ)研究函数 (常数
(常数 )在定义域内的单调性,并说明理由;
)在定义域内的单调性,并说明理由;
(Ⅲ)若把函数 (常数
(常数 )在[1,2]上的最小值记为
)在[1,2]上的最小值记为 ,
,
求 的表达式
的表达式
(本小题满分12分)
设函数 其中实
其中实 数
数 。
。
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)当函数 与
与 的图象只有一个公共点时,记
的图象只有一个公共点时,记 的最小值为
的最小值为 ,求
,求 的值域;
的值域;
(Ⅲ)若 与
与 在区间
在区间 内均
内均 为增函数,求
为增函数,求 的取值范围
的取值范围