(本小题满分14分)
设数列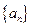 的前
的前 项和为
项和为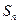 ,且对任意的
,且对任意的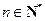 ,都有
,都有 ,
, .
.
(1)求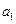 ,
,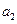 的值;(2)求数列
的值;(2)求数列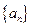 的通项公式
的通项公式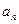 ;(3)证明:
;(3)证明: .
.
(本小题满分12分)
已知椭圆C的焦点F1(- ,0)和F2(
,0)和F2( ,0),长轴长6,设直线
,0),长轴长6,设直线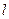 交椭圆C于A
交椭圆C于A B
B 两点,且线段AB的中点坐标是P(-
两点,且线段AB的中点坐标是P(-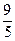 ,
,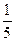 ),求直线
),求直线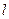 的方程。
的方程。
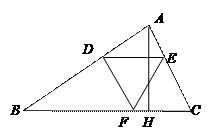
(课改班做) 如图5,等边△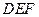 内接于△
内接于△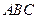 ,且DE//BC,已知
,且DE//BC,已知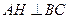 于点H,BC=4,AH=
于点H,BC=4,AH=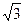 ,求△
,求△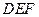 的边长.
的边长.
(本小题满分10分)
(平行班做)已知抛物线 y ="x2" -4与直线y =" x" + 2。
(1)求两曲线的交点;
(2)求抛物线 在交点处的切线方程。
在交点处的切线方程。
(本小题满分12分)
已知在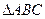 中,角
中,角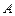 ,
,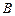 ,
,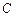 的对边的边长分别为
的对边的边长分别为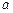 ,
,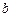 ,
,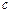 ,且
,且
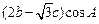 .
.
(Ⅰ)求角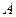 的大小;
的大小;
(Ⅱ)现给出三个条件:①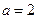 ;②
;②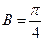 ;③
;③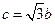 .
.
试从中选出两个可以确定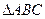 的条件,写出你的选择,并以此为依据求出
的条件,写出你的选择,并以此为依据求出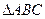
 的面积.(只需写出一个选定方案即可,选多种方案以第一种方案记分)
的面积.(只需写出一个选定方案即可,选多种方案以第一种方案记分)
(本小题满分10分)选修4-5:不等式选讲
设 (
( ).
).
(Ⅰ)当 时,求函数
时,求函数 的定义域;
的定义域;
(Ⅱ)若当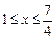 ,
, 恒成立,求实数
恒成立,求实数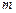 的取值范围.
的取值范围.