如图所示,轻绳绕过轻滑轮连接着边长为L的正方形导线框A1和物块A2,线框A1的电阻为R,质量为M,物块A2的质量为m(M>m),两匀强磁场区域I、II的高度也为L,磁感应强度均为B,方向水平与线框平面垂直。线框ab边距磁场边界高度为h。开始时各段绳都处于伸直状态,把它们由静止释放,ab边刚穿过两磁场的分界线CC/进入磁场II时线框做匀速运动。求:
(1)ab边刚进入磁场I时线框A1的速度v1;
(2)ab边进入磁场II后线框A1其重力的功率P;
(3)从ab边刚进入磁场II到ab边刚穿出磁场II的过程中,线框中产生的焦耳热Q。
通过“30m折返跑”的测试成绩可以反应一个人的身体素质.在平直的跑道上,一学生站立在起点线处,当听到起跑口令后(测试员同时开始计时),跑向正前方30m处的折返线,到达折返线处时,用手触摸固定在折返线处的标杆,再转身跑回起点线,返程无需减速,到达起点线处时,停止计时,全过程所用时间即为折返跑的成绩.学生可视为质点,加速或减速过程均视为匀变速,触摸杆的时间不计.该学生加速时的加速度大小为a1=2.5m/s2,减速时的加速度大小为a2=5m/s2,到达折返线处时速度需减小到零,并且该生全过程中最大速度不超过vm=12m/s.求该学生“30m折返跑”的最好成绩.
如图所示,空间分布着图示的匀强电场E(宽为L)和匀强磁场B,一带电粒子质量为m,电量为q,(不计重力)从A点由静止释放后经电场加速后进入磁场,穿过中间磁场进入右边磁场后能按某一路径再返回A点而重复前述过程.求中间磁场的宽度d和粒子的运动周期(虚线为磁场分界线,并不表示有什么障碍物)
在相互垂直的匀强电场和匀强磁场中,有一倾角为θ,足够长的光滑绝缘斜面,磁感强度为B,方向垂直纸面向外,电场方向竖直向上.有一质量为m,带电挝为十q的小球静止在斜面顶端,这时小球对斜面的正压力恰好为零,如图所示,若迅速把电场方向反转竖直向下,小球能在斜面上连续滑行多远?所用时间是多少?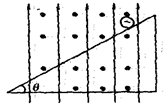
如图,质量m、初速υ0的电子束从电容器左边正中间O处水平射入,在电场力的作用下以速度υ,从C点射出。若电场不变,再加一个垂直于纸面向里的磁场,则电子从d点射出,c、d关于水平线从对称,则从d点射出时电子动能为多少?