已知抛物线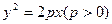 .过动点M(
.过动点M(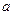 ,0)且斜率为1的直线
,0)且斜率为1的直线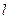 与该抛物线交于不同的两点A、B,
与该抛物线交于不同的两点A、B,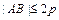 .
.
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)若线段AB的垂直平分线交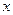 轴于点N,求
轴于点N,求 面积的最大值.
面积的最大值.
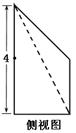
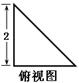
(本小题满分12分)如图是某直三棱柱被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点,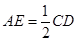 ,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.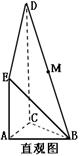
(Ⅰ)求证: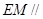 平面
平面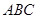 ;
;
(Ⅱ)求出该几何体的体积;
(Ⅲ)试问在边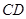 上是否存在点N,使
上是否存在点N,使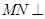 平面
平面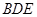 ? 若存在,确定点N的位置;若不存在,请说明理由.
? 若存在,确定点N的位置;若不存在,请说明理由.
(本小题满分12分)某校为进行爱国主义教育,在全校组织了一次有关钓鱼岛历史知识的竞赛.现有甲、乙两队参加钓鱼岛知识竞赛,每队3人,规定每人回答一个问题,答对为本队赢得1分,答错得0分.假设甲队中每人答对的概率均为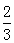 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为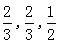 ,且各人回答正确与否相互之间没有影响,用ξ表示甲队的总得分.
,且各人回答正确与否相互之间没有影响,用ξ表示甲队的总得分.
(Ⅰ)求随机变量ξ的分布列和数学期望;
(Ⅱ)用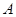 表示“甲、乙两个队总得分之和等于3”这一事件,用
表示“甲、乙两个队总得分之和等于3”这一事件,用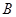 表示“甲队总得分大于乙队总得分” 这一事件,求
表示“甲队总得分大于乙队总得分” 这一事件,求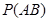 .
.
(本小题满分12分)已知向量 ,
,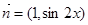 ,函数
,函数 .
.
(Ⅰ)求函数f (x)的最小正周期和单调递减区间;
(Ⅱ)在 中,
中,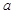 ,
, ,
, 分别是角
分别是角 ,
, ,
,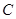 的对边,且
的对边,且 ,
, ,
, 的面积为
的面积为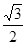 ,且a > b,求
,且a > b,求 的值.
的值.
(本小题满分14分)已知函数 .
.
(Ⅰ)求证:曲线 在点
在点 处的切线在
处的切线在 轴上的截距为定值;
轴上的截距为定值;
(Ⅱ)若 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知椭圆 :
: 与抛物线
与抛物线 :
: 有相同焦点
有相同焦点 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)已知直线 过椭圆
过椭圆 的另一焦点
的另一焦点 ,且与抛物线
,且与抛物线 相切于第一象限的点
相切于第一象限的点 ,设平行
,设平行 的直线
的直线 交椭圆
交椭圆 于
于 两点,当△
两点,当△ 面积最大时,求直线
面积最大时,求直线 的方程.
的方程.