已知方向向量为
的直线
过椭圆C：＝1(a＞b＞0)的焦点以及点(0，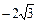
)，椭圆C的中心关于直线的对称点在椭圆C的右准线上。
⑴求椭圆C的方程。
⑵过点E(-2，0）的直线
交椭圆C于点M、N，且满足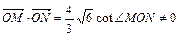
，(O为坐标原点)，求直线的方程。
计算下列各题
（1）
；
（2）
+
.
已知复数z1=m+(4-m2)i(m∈R),z2=2cos
+(
+3sin)i (∈R).若z1=z2,求的取值范围.
已知m∈R，复数z=
+(m2+2m-3)i,当m为何值时，（1）z∈R；（2）z是纯虚数；（3）z对应的点位于复平面第二象限；（4）z对应的点在直线x+y+3=0上.
是否存在常数a、b、c使等式12+22+32+…+n2+（n-1）2+…+22+12=an（bn2+c）对于一切n∈N*都成立，若存在，求出a、b、c并证明；若不存在，试说明理由.
数列{an}满足Sn=2n-an(n∈N*).
(1)计算a1,a2,a3,a4,并由此猜想通项公式an;
（2）用数学归纳法证明（1）中的猜想.