利用反应堆工作时释放出的热能使水汽化以推动汽轮发电机发电，这就是核电站.核电站消耗的“燃料”很少，但功率却很大.目前，核能发电技术已经成熟，我国已具备了发展核电的基本条件.
（1）核反应堆中的“燃料”是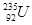
，完成下面的核反应方程式
.
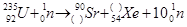(2)一座100万千瓦的核电站，每年需要多少吨浓缩铀？已知铀核的质量为235.043 9 u，中子质量为1.008 7 u，锶（Sr）核的质量为89.907 7 u，氙（Xe）核的质量为135.907 2 u，1 u=1.66×10-27 kg，浓缩铀中铀235的含量占2％.
(3)同样功率（100万千瓦）的火力发电站，每年要消耗多少吨标准煤？(已知标准煤的热值为2.93×104 kJ/kg)
(4)为了防止铀核裂变产物放出的各种射线对人体的危害和对环境的污染，需采取哪些措施？（举两种）
有人在游泳池边上竖直向下观察池水的深度，看到池水的深度约为h。已知水的折射率n=4/3,那么，水的实际深度约为多少？
如图13-1-12所示，游泳池宽度L="15" m，水面离岸边的高度为0.5 m，在左岸边一标杆上装有一A灯，A灯距地面高0.5 m，在右岸边站着一个人，E点为人眼的位置，人眼距地面高1.5 m.若此人发现A灯光经水面反射所成的像与左岸水面下某处的B灯光经折射后所成的像重合，已知水的折射率为1.3，则B灯在水面下多深处？（B灯在图中未画出）
图13-1-12
如图13-1-11所示，光线以入射角θ1从空气射向折射率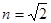
的玻璃表面.
图13-1-11
（1）当入射角θ1=45°时，反射光线与折射光线间的增值角θ为多少？
（2）当入射角θ1为多少时，反射光线和折射光线垂直？
如图13-1-9所示，水面上漂浮着一半径为r的圆形薄木板，在木板圆心的正上方距木板高度h的A处有一个点光源S.由于木板的影响，点光源发出的光线射入水中后，在水底平面上形成一圆形阴影.已知水深为H，水的折射率为n，求阴影的半径.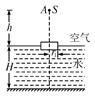
图13-1-9
在折射率为n、厚度为d的玻璃平板上方的空气中有一点光源S，从S发出的光线SA以入射角θ入射到玻璃板上表面，经过玻璃板后从下表面射出，如图19-2-13所示.若沿此光线传播的光从光源到玻璃板上表面的传播时间与在玻璃板中的传播时间相等，点光源S到玻璃板上表面的垂直距离l应是多少？