已知椭圆的一个焦点F1(0,-2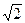 ),对应的准线方程为y=-
),对应的准线方程为y=- ,且离心率e满足:
,且离心率e满足: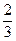 ,e,
,e,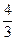 成等比数列.
成等比数列.
(1)求椭圆方程;
(2)是否存在直线l,使l与椭圆交于不同的两点M、N,且线段MN恰被直线x=-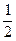
平分.若存在,求出l的倾斜角的范围;若不存在,请说明理由.
已知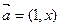 ,
, ,m<-2,求使
,m<-2,求使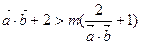 成立的x的取值
成立的x的取值
范围。
投资生产A产品时,每生产100吨需要资金200万元,需场地200m2,可获利润300万元,投资生产B产品时,每生产100吨需资金300万元,需场地100m2,可获利润200万元,某单位有可使用资金1400万元,场地900 m2,问作怎样的组合可获利最多?最多利润是多少?
| 资金(万元) |
场地(m2) |
利润(万元) |
|
| A产品(每百吨) |
200 |
200 |
300 |
| B产品(每百吨) |
300 |
100 |
200 |
在△ABC中,a、b、c成等比数列,
①求A的大小;②求sinB的取值范围。
已知集合
 ,求a的取值范围。
,求a的取值范围。
(满分14分)
设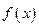 的定义域为
的定义域为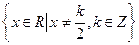 ,且
,且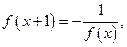 如果
如果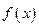 为奇函数,当
为奇函数,当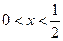 时,
时,
(1)求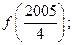
(2)当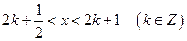 时,求
时,求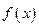
(3)是否存在这样的自然数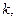 使得当
使得当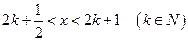 时,
时,
不等式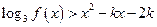 有实数解.
有实数解.