已知函数 ,其中a为常数,且
,其中a为常数,且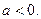
(1)若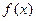 是奇函数,求a的取值集合A;
是奇函数,求a的取值集合A;
(2)当a=-1时,设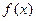 的反函数为
的反函数为 ,且函数
,且函数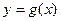 的图像与
的图像与 的图像关于
的图像关于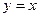 对称,求
对称,求 的取值集合B。
的取值集合B。
(3)对于问题(1)(2)中的A、B,当 时,不等式
时,不等式
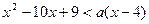 恒成立,求x的取值范围。
恒成立,求x的取值范围。
已知函数 .
.
(1)当 时,求证:
时,求证: ;
;
(2)当 时,
时, 恒成立,求实数
恒成立,求实数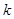 的值.
的值.
已知椭圆 的离心率为
的离心率为 ,长轴
,长轴 ,短轴
,短轴 ,四边形
,四边形 的面积为
的面积为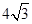 .
.
(1)求椭圆的方程;
过椭圆的右焦点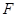 的直线
的直线 交椭圆于
交椭圆于 ,直线
,直线
 .
.
①证明: ,并求直线
,并求直线 的方程;②证明:以
的方程;②证明:以 为直径的圆过右焦点
为直径的圆过右焦点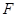 .
.
数列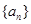 的通项
的通项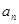 是关于
是关于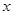 的不等式
的不等式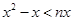 的解集中正整数的个数,
的解集中正整数的个数,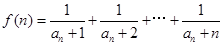 .
.
(1)求数列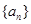 的通项公式;(2)若
的通项公式;(2)若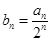 ,求数列
,求数列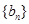 的前
的前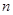 项和
项和 ;
;
(3)求证:对 且
且 恒有
恒有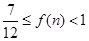 .
.
已知四棱锥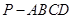 ,底面
,底面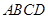 是菱形,
是菱形,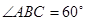 ,
, ,
, .
.
(1)求证: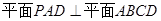 ;
;
(2)求二面角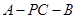 的余弦值.
的余弦值.
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组
区间是: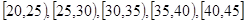 .
.
(1)求图中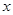 的值并根据频率分布直方图估计这500名志愿者中年龄在
的值并根据频率分布直方图估计这500名志愿者中年龄在 岁的人数;
岁的人数;
(2)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动,再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.