已知点A
,动点
在双曲线
上运动,且
,求点P的轨迹方程.
已知△
中，
，
，
平面，
，
、
分别是
、
上的动点，且
．
（1）求证：不论
为何值，总有平面
平面
；
（2）当为何值时，平面平面
？
已知多面体
中， 四边形
为矩形，
，
，平面
平面， 
、
分别为
、
的中点，且
，
.
（1）求证：
平面
；
（2）求证：
平面
；
（3）设平面
将几何体
分成的两个锥体的体积分别为
，
，求
的值.
已知函数
．
（1）若
在
上存在零点，求实数
的取值范围；
（2）当
时，若对任意的
，总存在
使
成立，求实数
的取值范围．
如图，椭圆
过点P(1, 
)，其左、右焦点分别为F1,F2,离心率e＝
, M, N是直线x＝4上的两个动点，且
·
＝0.
（1）求椭圆的方程；
（2）求MN的最小值；
（3）以MN为直径的圆C是否过定点？
已知函数f(x)＝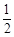
ax2－(2a＋1)x＋2lnx(a∈R).
（1）若曲线y＝f(x)在x＝1和x＝3处的切线互相平行，求a的值；
（2）当a≤0时，求f(x)的单调区间。