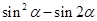设直线 . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.
(Ⅰ)已知函数 .求证:
.求证: 为曲线
为曲线 的“上夹线”.
的“上夹线”.
(Ⅱ)观察下图:
根据上图,试推测曲线 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.
(本小题满分10分)如图所示,在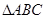 中,
中,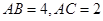 ,若
,若 为
为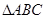 的外心.
的外心.
(Ⅰ)求 的值;
的值;
(Ⅱ)求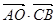 的值;
的值;
(Ⅲ)若平面内一点 满足
满足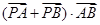
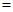

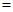

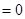 ,试判定点
,试判定点 的位置.
的位置.
(本小题满分8分)已知向量 不共线,
不共线, 为实数.
为实数.
(Ⅰ)若 ,
, ,
, ,当
,当 为何值时,
为何值时, 三点共线;
三点共线;
(Ⅱ)若 ,且
,且 与
与 的夹角为
的夹角为 ,实数
,实数 ,求
,求  的取值范围.
的取值范围.
(本小题满分8分)从某校高一年级800名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米和195厘米之间,将测量结果分为八组:第一组 ,第二组
,第二组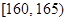 ,……,第八组
,……,第八组 ,得到频率分布直方图如右.
,得到频率分布直方图如右.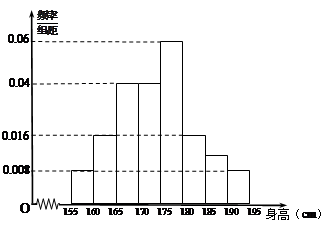
(Ⅰ)计算第七组[185,190)的样本数;并估计这个高一年级800名学生中身高在170厘米以下的人数;
(Ⅱ) 求出这100名学生身高的中位数、平均数.
(本小题满分7分)将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为 ,第二次出现的点数为
,第二次出现的点数为 .
.
(Ⅰ)求事件 的概率;
的概率;
(Ⅱ)求事件“点 在圆
在圆 面上”(包括边界)的概率.
面上”(包括边界)的概率.
(本小题满分7分)已知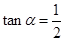 ,求下列式子的值.
,求下列式子的值.
(1)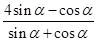
(2)