(本小题满分7分)将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为 ,第二次出现的点数为
,第二次出现的点数为 .
.
(Ⅰ)求事件 的概率;
的概率;
(Ⅱ)求事件“点 在圆
在圆 面上”(包括边界)的概率.
面上”(包括边界)的概率.
袋中有大小、形状相同的红、黑球各一个,现一次有放回地随机摸取3次,每次摸取一个球。
(1)试问:一共有多少种不同的结果?请列出所有可能的结果;
(2)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率。
已知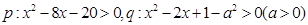 .若
.若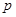 是
是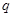 的充分而不必要条件,求正实数
的充分而不必要条件,求正实数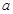 的取值范围。
的取值范围。
已知函数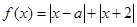 (a为常数,且a∈R).
(a为常数,且a∈R).
(1)若函数f (x)的最小值为2,求a的值;
(2)当a=2时,解不等式f (x)≤6.
在极坐标系中,已知两点O(0,0),B(2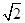 ,
,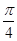 ).
).
(1)求以OB为直径的圆C的极坐标方程,然后化成直角方程;
(2)以极点O为坐标原点,极轴为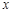 轴的正半轴建立平面直角坐标系,直线l的参数方程为
轴的正半轴建立平面直角坐标系,直线l的参数方程为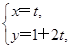 (t为参数).若直线l与圆C相交于M,N两点,圆C的圆心为C,求DMNC的面积.
(t为参数).若直线l与圆C相交于M,N两点,圆C的圆心为C,求DMNC的面积.
如图,已知C、F是以AB为直径的半圆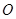 上的两点,且CF=CB,过C作CD^AF交AF的延长线与点D.
上的两点,且CF=CB,过C作CD^AF交AF的延长线与点D.
(1)证明:CD为圆O的切线;
(2)若AD=3,AB=4,求AC的长.