F1、F2为双曲线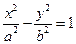 的左右焦点,O为坐标原点,P在双曲线的左支上,点M在右准线上,且满足:
的左右焦点,O为坐标原点,P在双曲线的左支上,点M在右准线上,且满足: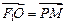 ,
,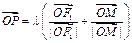 (λ>0)
(λ>0)
(1)求此双曲线的离心率;
(2)若过点N(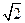 ,
,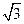 )的双曲线C的虚轴端点分别为B1、B2(B1在y轴正半轴上),点A、B在双曲线上,且
)的双曲线C的虚轴端点分别为B1、B2(B1在y轴正半轴上),点A、B在双曲线上,且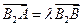 ,
,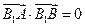 ,求双曲线C和直线AB的方程。
,求双曲线C和直线AB的方程。
选修4-5:不等式选讲
若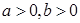 ,且
,且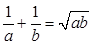 .
.
(Ⅰ)求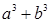 的最小值;
的最小值;
(Ⅱ)是否存在 ,使得
,使得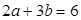 ?并说明理由.
?并说明理由.
选修4-4:坐标系与参数方程
在直角坐标系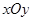 中,直线
中,直线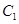 :
:
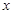 =
=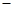 2,圆
2,圆 :
: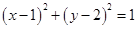 ,以坐标原点为极点,
,以坐标原点为极点,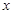 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(Ⅰ)求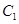 ,
, 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线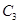 的极坐标方程为
的极坐标方程为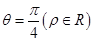 ,设
,设 与
与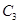 的交点为
的交点为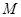 ,
, ,求
,求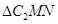 的面积.
的面积.
选修4-1:几何证明选讲
如图,四边形 是
是 的内接四边形,
的内接四边形, 的延长线与
的延长线与 的延长线交于点
的延长线交于点 ,且
,且 .
.
(Ⅰ)证明: ;
;
(Ⅱ)设 不是
不是 的直径,
的直径, 的中点为
的中点为 ,且
,且 ,证明:
,证明: 为等边三角形.
为等边三角形.
已知函数f(x)=x2+ax+b,g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(Ⅰ)求a,b,c,d的值;
(Ⅱ)若x≥-2时,f(x)≤kg(x),求k的取值范围.
如图,三棱柱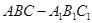 中,侧面
中,侧面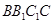 为菱形,
为菱形,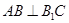 .
.
(Ⅰ)证明: ;
;
(Ⅱ)若 ,
,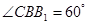 ,
,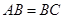 ,求二面角
,求二面角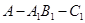 的余弦值.
的余弦值.