选修4-1:几何证明选讲
如图,四边形 是
是 的内接四边形,
的内接四边形, 的延长线与
的延长线与 的延长线交于点
的延长线交于点 ,且
,且 .
.
(Ⅰ)证明: ;
;
(Ⅱ)设 不是
不是 的直径,
的直径, 的中点为
的中点为 ,且
,且 ,证明:
,证明: 为等边三角形.
为等边三角形.
做一个圆柱形锅炉,容积为V,两个底面的材料每单位面积的价格为a元,侧面的材料每单位面积价格为b元,问锅炉的底面直径与高的比为多少时,造价最低?
证明不等式:若x>0,则ln(1+x)>
计算下列定积分
(1) (2)
(2)
(本小题满分15分)已知函数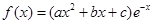
 的图像过点
的图像过点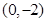 ,且在该点的切线方程为
,且在该点的切线方程为 .
.
(Ⅰ)若 在
在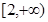 上为单调增函数,求实数
上为单调增函数,求实数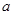 的取值范围;
的取值范围;
(Ⅱ)若函数 恰好有一个零点,求实数
恰好有一个零点,求实数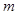 的取值范围.
的取值范围.
(本小题满分15分)
已知椭圆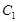 :
: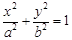 (
(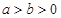 )的离心率为
)的离心率为 ,直线
,直线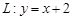 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆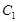 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
(1)求椭圆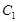 的方程;
的方程;
(2)设椭圆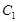 的左焦点为
的左焦点为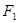 ,右焦点为
,右焦点为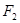 ,直线
,直线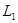 过点
过点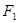 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线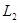 垂直
垂直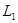 于点
于点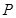 ,线段
,线段 的垂直平分线交
的垂直平分线交 于点
于点 .
.
(i)求点 的轨迹
的轨迹 的方程;
的方程;
(ii)若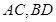 为点
为点 的轨迹
的轨迹 的过点
的过点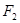 的两条相互垂直的弦,求四边形
的两条相互垂直的弦,求四边形 面积的最小值.
面积的最小值.