已知函数
(I)若函数 的图象关于直线
的图象关于直线 对称,求a的最小值;
对称,求a的最小值;
(II)若存在 成立,求实数m的取值范围.
成立,求实数m的取值范围.
正实数数列
中,
,且
成等差数列.
(1) 证明数列
中有无穷多项为无理数;
(2)当
为何值时,
为整数,并求出使
的所有整数项的和.
已知抛物线
经过椭圆
的两个焦点. 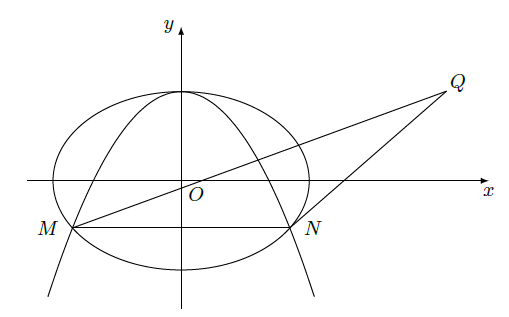
(1) 求椭圆
的离心率;
(2) 设
,又
为
与
不在
轴上的两个交点,若
的重心在抛物线
上,求
和
的方程.
如图, 与 都是边长为2的正三角形,平面 平面 , 平面 ,

(1)求直线
与平面
所成的角的大小;
(2)求平面
与平面
所成的二面角的正弦值.
已知函数
.
(1)若
,求
;
(2)若
,求
的取值范围.