已知: (
( )是方程
)是方程 的两根,且
的两根,且 ,
, .
.  (1)求
(1)求 的值;(2)设
的值;(2)设 ,求证:
,求证: ;(3)求证:对
;(3)求证:对 有
有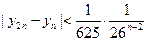 w。.w..
w。.w..
B(选修4—2:矩阵与变换)
已知 ,向量
,向量 是矩阵
是矩阵 的属性特征值
的属性特征值 的一个特征向量,矩阵
的一个特征向量,矩阵 以及它的另一个特征值.
以及它的另一个特征值.
【2015江苏高考,21】A(选修4—1:几何证明选讲)
如图,在 中,
中, ,
, 的外接圆圆O的弦
的外接圆圆O的弦 交
交 于点D
于点D
求证: ∽
∽
【2015高考新课标2,理24】(本小题满分10分)选修4-5不等式选讲
设 均为正数,且
均为正数,且 ,证明:
,证明:
(Ⅰ)若 ,则
,则 ;
;
(Ⅱ) 是
是 的充要条件.
的充要条件.
【2015高考新课标2,理23】选修4-4:坐标系与参数方程
在直角坐标系 中,曲线
中,曲线 (
( 为参数,
为参数, ),其中
),其中 ,在以
,在以 为极点,
为极点, 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线 ,曲线
,曲线 .
.
(Ⅰ)求 与
与 交点的直角坐标;
交点的直角坐标;
(Ⅱ)若 与
与 相交于点
相交于点 ,
, 与
与 相交于点
相交于点 ,求
,求 的最大值.
的最大值.
【2015高考新课标2,理22】选修4—1:几何证明选讲
如图, 为等腰三角形
为等腰三角形 内一点,圆
内一点,圆 与
与 的底边
的底边 交于
交于 、
、 两点与底边上的高
两点与底边上的高 交于点
交于点 ,与
,与 、
、 分别相切于
分别相切于 、
、 两点.
两点.
(Ⅰ)证明: ;
;
(Ⅱ)若 等于
等于 的半径,且
的半径,且 ,求四边形
,求四边形 的面积.
的面积.