1)设函数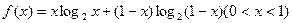 ,求
,求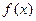 的最小值;
的最小值;
(2)设正数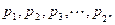 满足
满足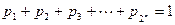 ,
,
求证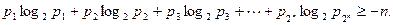
.(本小题满分12分)
在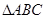 中,
中,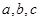 分别是
分别是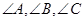 的对边长,已知
的对边长,已知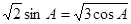 .
.
( 1 ) 若 ,求实数
,求实数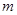 的值;
的值;
( 2 ) 若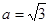 ,求
,求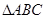 面积的最大值.
面积的最大值.
已知数列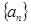 中,
中,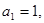 且点
且点 在直线
在直线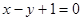 上。
上。
(Ⅰ)求数列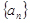 的通项公式;
的通项公式; (Ⅱ)若函数
(Ⅱ)若函数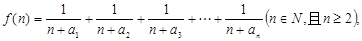 求函数
求函数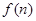 的最小值;
的最小值; (Ⅲ)设
(Ⅲ)设 表示数列
表示数列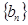 的前
的前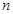 项和。试问:是否存在关于
项和。试问:是否存在关于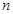 的整式
的整式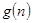 ,使得
,使得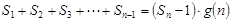 对于一切不小于2的自然数
对于一切不小于2的自然数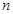 恒成立? 若存在,写出
恒成立? 若存在,写出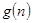 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。
设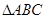 的内角
的内角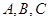 所对的边分别为
所对的边分别为 且
且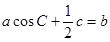 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若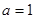 ,求
,求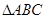 的周长
的周长 的取值范围.
的取值范围.
已知数列 的前
的前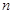 项和为
项和为 ,
, ,且
,且 (
(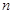 为正整数)
为正整数)
(Ⅰ)求出数列 的通项公式;
的通项公式;
(Ⅱ)若对任意正整数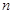 ,
, 恒成立,求实数
恒成立,求实数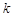 的最大值.
的最大值.
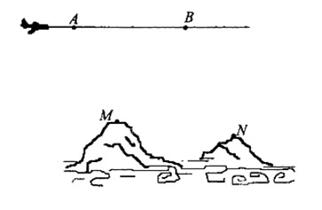
为了测量两山顶M,N间的距离,飞机沿水平方向在A,B两点进行测量,A,B,M,N在同一个铅垂平面内(如示意图),飞机能够测量的数据有俯角和A,B间的距离,请设计一个方案,包括:①指出需要测量的数据(用字母表示,并在图中标出);②用文字和公式写出计算M,N间的距离的步骤。