(本小题满分12分)在边长为60 cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大容积是多少?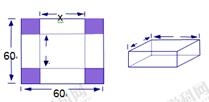
(本小题满分10分)在直角坐标系xOy中,直线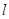 的参数方程为
的参数方程为 (
(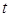 为参数).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以
为参数).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以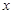 轴正半轴为极轴)中,圆C的方程为ρ=2
轴正半轴为极轴)中,圆C的方程为ρ=2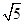 sinθ.
sinθ.
(1)求圆C的直角坐标方程;
(2)设圆C与直线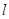 交于点
交于点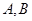 .若点
.若点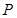 的坐标为(3,
的坐标为(3,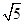 ),求
),求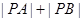 .
.
(本小题满分12分)如图,在三棱柱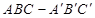 中,侧面
中,侧面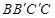 为菱形,
为菱形,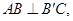

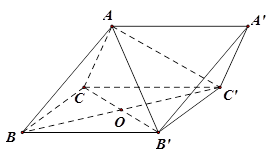
(1)求证:平面 平面
平面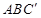 ;
;
(2)若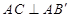 ,
, ,求四棱锥
,求四棱锥 的体积。
的体积。
(本小题满分12分)如图,在四棱锥 中,底面
中,底面 为直角梯形,且
为直角梯形,且 ,
, ,侧面
,侧面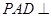 底面
底面 . 若
. 若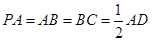 .
. (1)求证:
(1)求证: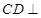 平面
平面 ;
;
(2)侧棱 上是否存在点
上是否存在点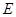 ,使得
,使得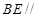 平面
平面 ?若存在,指出点
?若存在,指出点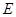 的位置并证明;若不存在,请说明理由。
的位置并证明;若不存在,请说明理由。
(本小题满分12分)如图(1),在直角梯形 中,
中,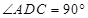 ,
, ,
,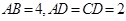 .将
.将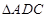 沿
沿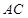 折起,使平面
折起,使平面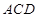
 平面
平面 ,得到几何体
,得到几何体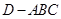 ,如图所示(2).
,如图所示(2).
(Ⅰ)求证: 平面
平面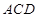 ;
;
(Ⅱ)求几何体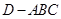 的体积.
的体积.