(本小题满分12分)
设函数f(x)=ax+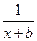 (a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方程为y=3。
(a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方程为y=3。
(Ⅰ)求f(x)的解析式:
(Ⅱ)证明:函数y=f(x)的图像是一个中心对称图形,并求其对称中心;
(Ⅲ)证明:曲线y=f(x)上任一点的切线与直线x=1和直线y=x所围三角形的面积为定值,并求出此定值。
某社区的常住人口中,有成年人3200人,其中有无业人员1000人,从事个体劳动的有1160人,有固定收入的上班人员1040人,如果想通过调查其中160人的生活消费情况来了解本社区群众的生活消费情况,考虑到由于各种人员情况的差异,而同一阶层人员的差异较小,问应当采取怎样的抽取方法?从事个体劳动的人员中应抽查多少人?在本问题的设计中还有哪些重要因素将影响调查效果?应怎样改进抽查方案使效果更加客观?
一批车床中有甲厂生产的56台,乙厂生产的42台,用分层抽样法从中抽取14台车床,请写出过程.
已知函数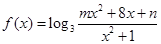 的定义域为
的定义域为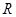 ,值域为
,值域为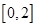 ,求
,求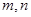 的值。
的值。
已知函数 ,
,
(1)求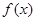 的定义域;
的定义域;
(2)判断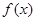 的奇偶性。
的奇偶性。
已知函数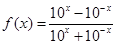 ,判断
,判断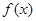 的奇偶性和单调性。
的奇偶性和单调性。