随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元。设1件产品的利润(单位:万元)为
。
(1)求
的分布列;
(2)求1件产品的平均利润(即
的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品提高为70%.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
已知集合A={x|ax2-3x+2=0,a∈R}.
(1) 若A是空集,求a的取值范围;
(2) 若A中只有一个元素,求a的值,并将这个元素写出来;
(3) 若A中至多有一个元素,求a的取值范围.
已知函数f(x)=lnx-ax2+(2-a)x.
(1)讨论f(x)的单调性;
(2)设a>0,证明:当0<x<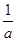 时,f
时,f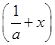 >f
>f ;
;
(3)若函数y=f(x)的图象与x轴交于A、B两点,线段AB中点的横坐标为x0,证明: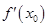 <0.
<0.
已知函数f(x)=ax+x2-xlna(a>0,a≠1).
(1)当a>1时,求证:函数f(x)在(0,+∞)上单调递增;
(2)若函数y=|f(x)-t|-1有三个零点,求t的值;
(3)若存在x1、x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1,试求a的取值范围.
定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界.已知函数f(x)=1+a·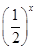 +
+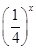 .
.
(1)当a=1时,求函数f(x)在(-∞,0)上的值域,并判断函数f(x)在(-∞,0)上是否为有界函数,请说明理由;
(2)若函数f(x)在[0,+∞)上是以3为上界的有界函数,求实数a的取值范围.
已知f(x)=xlnx,g(x)=-x2+ax-3.
(1)求函数f(x)在[t,t+2](t>0)上的最小值;
(2)对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围;
(3)证明对一切x∈(0,+∞),都有lnx>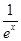 -
-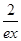 成立.
成立.