设函数
,曲线
在点
处的切线方程为
.
(Ⅰ)求
的解析式:
(Ⅱ)证明:函数
的图像是一个中心对称图形,并求其对称中心;
(Ⅲ)证明:曲线
上任一点的切线与直线
和直线
所围三角形的面积为定值,并求出此定值.
(本小题满分14分)向量 满足
满足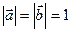 ,
,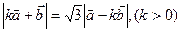 .
.
(1)求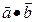 关于k的解析式
关于k的解析式 ;
;
(2)请你分别探讨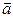 ⊥
⊥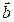 和
和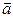 ∥
∥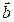 的可能性,若不可能,请说明理由,若可能,求出k的值;
的可能性,若不可能,请说明理由,若可能,求出k的值;
(3)求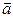 与
与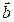 夹角的最大值.
夹角的最大值.
(本小题满分12分)某租赁公司有汽车100辆,当每辆车月租金为3000元时,可全租出,当每辆车月租金每增加50元,未租出的车将会增加 一辆.
一辆. 租出的车每辆每月需维护费150元,未租出的车每辆每月需维护费50元.
租出的车每辆每月需维护费150元,未租出的车每辆每月需维护费50元.
(1)当每辆车月租金定为3600元时,能租出多少辆车?此时的月收益是多少?
(2)每辆车的月租金定为多少元时,租赁公司的月收益最大?
(本小题满分12分)已知集合A=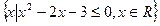 ,集合B=
,集合B=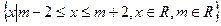 .
.
(1)若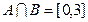 ,求实数m的值;
,求实数m的值;
(2)若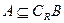 ,求实数m的取值范围.
,求实数m的取值范围.
有n2(n≥4)个正数,排成n×n矩阵(n行n列的数表),其中每一行的数成等差数列,每一列的数成等比数列,并且所有公比都相等,且满足a24=1,a42=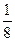 ,a43=
,a43= ,
,
求:(1)公比q;
(2)用k表示a4k;
(3)求a11+a22+a33+…+ann的值。
△ABC中,AB= ,AC边上的中线BD=
,AC边上的中线BD=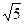 ,cosB=
,cosB= ,如图所示,
,如图所示,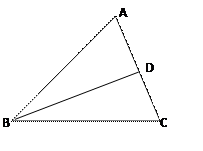 求:sinA。
求:sinA。