如图,在棱长为2的正方体 中, 是 的中点,求直线 与平面 所成角的大小(结果用反三角函数表示).

已知集合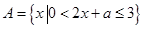 ,
, .
.
(1)当 时,求
时,求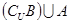 ;.
;.
(2)若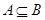 ,求实数
,求实数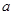 的取值范围.
的取值范围.
计算下列各式:(要求写出必要的运算步骤)
(1)
(2)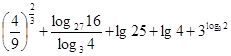 .
.
已知集合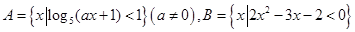 .
.
(1)求集合 ;
;
(2)求证: 的充要条件为
的充要条件为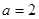 ;
;
(3)若命题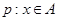 ,命题
,命题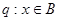 且
且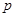 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.
已知,命题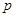 :
: ,命题
,命题 :
: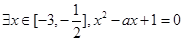 .
.
(1)若命题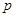 为真命题,求实数
为真命题,求实数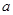 的取值范围;
的取值范围;
(2)若命题 为真命题,求实数
为真命题,求实数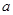 的取值范围;
的取值范围;
(3)若命题“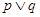 ”为真命题,且命题“
”为真命题,且命题“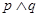 ”为假命题,求实数
”为假命题,求实数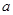 的取值范围.
的取值范围.
抽取某种型号的车床生产的10个零件,编号为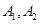 ,…,
,…,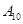 ,测量其直径(单位:cm),得到下面数据:
,测量其直径(单位:cm),得到下面数据:
| 编号 |
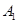 |
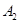 |
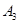 |
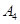 |
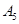 |
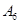 |
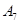 |
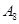 |
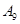 |
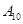 |
| 直径 |
1.51 |
1.49 |
1.49 |
1.51 |
1.49 |
1.48 |
1.47 |
1.53 |
1.52 |
1.47 |
其中直径在区间[1.49,1.51]内的零件为一等品.
(1)从上述10个零件中,随机抽取一个,求这个零件为一等品的概率;
(2)从一等品零件中,随机抽取2个.
①用零件的编号列出所有可能的抽取结果;
②求这2个零件直径相等的概率;
(3)若甲、乙分别从一等品中各取一个,求甲取到零件的直径大于乙取到零件的直径的概率.